1. 针孔模型
1.1 小孔成像
相机可以抽象为最简单的形式:一个小孔和一个成像平面,小孔位于成像平面和真实的三维场景之间。
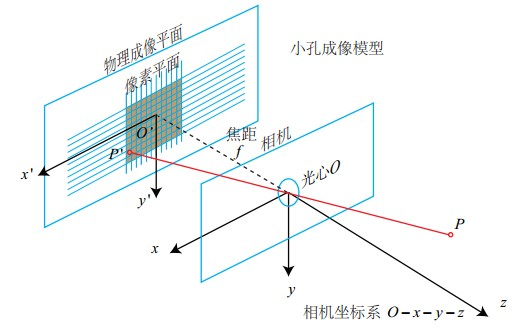
描述小孔的成像过程前,首先来定义两个坐标系:
- 相机坐标系:相机的中心被称为焦点或者光心,以焦点$O_c$为原点和坐标轴$;X_c,Y_c,Z_c$组成了相机坐标系
- 图像坐标系:以成像平面$O’$为原点和坐标轴$x’,y’$组成了图像坐标系
小孔成像实际就是将相机坐标系中的三维点变换到成像平面中的图像坐标系中的二维点。
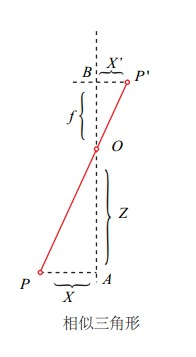
假设相机坐标系下P点的坐标为$P_c=[X,Y,Z]^T$,则其在图像坐标系下为$p=[x,y]^T$,由相似三角形可以得到:
1.2 内参数
从成像平面坐标系到像素坐标系的变换。上面推导中使用的像点坐标$p=(x,y)$是成像平面坐标系下,以成像平面的中心为原点。而实际像素点的表示方法是以像素来描述,坐标原点通常是图像的左上角,X轴沿着水平方向向左,Y轴竖直向下。
像素是一个矩形块,这里假设其在水平和竖直方向的长度分别为:α和β。所以像素坐标和成像平面坐标之间,相差了一个缩放和平移。
假设像素坐标的水平方向的轴为μ,竖直方向的轴为ν,那么将一个成像平面的坐标(x,y)在水平方向上缩放α倍,在竖直方向上缩放β倍,同时平移(cx,cy),就可以得到像素坐标系的坐标(μ,ν),其公式如下:
将上面求得的$(x,y)$带入上面公式可得到:
写成齐次坐标后:
通过上面的的推导,就得到了相机的内参数矩阵(Camera Intrinsic)K
$K$有4个未知数和相机的构造相关,$f_x,f_y$和相机的焦距,像素的大小有关;$c_x,c_y$是平移的距离。这些参数在出厂时就设置好,也可以用标定板确定。
1.3 外参数
通过上面的推导,知道了相机成像的过程:
其中,p是图像中像点的像素坐标,K是相机的内参数矩阵,P是相机坐标系下的三维点坐标。上面推导使用的三维点坐标是在相机坐标系下的,相机坐标系并是“不稳定”的坐标系,其会随着相机的移动而改变坐标的原点和各个坐标轴的方向。
因此需要引进一个稳定不变坐标系:世界坐标系,该坐标系是绝对不变,SLAM中的视觉里程计就是求解相机在世界坐标系下的运动轨迹。
设$P_c$是$P$在相机坐标系坐标,是$P_w$其在世界坐标系下的坐标,可以使用一个旋转矩阵和一个平移向量,将变换为:
改写为齐次形式就是:
上面就推导得到相机的外参数(Camera Extrinsic)T
1.4 内外参组合
$p=(\mu,\nu)$是图像中的像点,其坐标系是像素坐标系$P_c=(X_c,Y_c,Z_c)$是场景中的三维点,是相机坐标系。依托上面的公式,进过两次齐次化后,可以推导,像素坐标和世界坐标的关系:
2. 双目相机模型
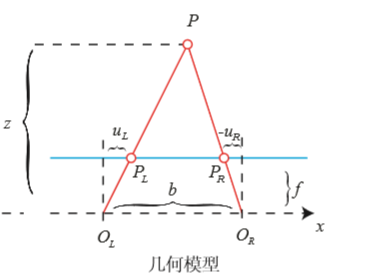
由相似三角形可知:
整理后可得:
$d$为左右图的横坐标之差,称为视差(Disparity)。根据视差,我们可以估计一个像素离相机的距离。视差与距离成反比:视差越大,距离越近
3. RGB-D相机模型
RGB-D相机是主动探测深度,一般分为结构光和脉冲光(TOF),也叫飞行时间法(Time of Flight)。
ToF 原理和激光传感器十分相似,不过激光是通过逐点扫描来获取距离,而 ToF 相机则可以获得整个图像的像素深度,这也正是 RGB-D 相机的特点。
我们可以在同一个图像位置, 读取到色彩信息和距离信息,计算像素的 3D 相机坐标,生成点云(Point Cloud)