SLAM基础8-建图

通过前端的信息采集，后端优化，回环优化后我们需要对信息汇总，最终形成一幅地图。本文介绍了SLAM中几种常见的建图策略。

在经典的 SLAM 模型中，我们所谓的地图，即所有路标点的集合。一旦我们确定了路标点的位置，那就可以说我们完成了建图，这就是所谓的稀疏路标地图。这种地图只建模感兴趣的部分，也就特征点（路标点），而稠密地图是指建模所有看到过的部分。

对于同一个桌子，稀疏地图可能只建模了桌子的四个角，而稠密地图则会建模整个桌面。虽然从定位角度看，只有四个角的地图也可以 用于对相机进行定位，但由于我们无法从四个角推断这几个点之间的空间结构，所以无法仅用四个角来完成导航、避障等需要稠密地图才能完成的工作。

1. 单目稠密建图

我们从最简单的情况开始：在给定相机轨迹的基础上，如何根据一段时间 的视频序列，来估计某张图像的深度。换言之，我们不考虑 SLAM，先考虑稍为简单的建图问题。

基本思路是：首先提特征，并根据描述子匹配。换言之，通过特征，我们对某一个空间点进行了跟踪，知道了它在各个图像之间的位置。 之后，通过不同视角下的观测，利用三角测量原理估计深度。

如何确定第一张图的某像素，出现在其他图里的位置呢？这需要用到极线搜索和块匹配技术。由于我们拍摄了多张图片，需要使用多次三角测量让深度逐渐收敛，需要使用深度滤波器技术。

1.1 极线搜索与块匹配

左边的相机观测到了像素$p_1$，由于这是一个单目相机，我们无法知道它的深度，因此该像素的空间点分布在图中的这条射线段上。由于知道了相机的运动，所以基线$O_1O_2$和极线$l_2$都是确定的。现在问题就变为：如何根据极线找到$p_2$的位置？由于单个像素不好判断，所以为了提高区分度需要使用块匹配。

我们在$p_1$周围取$w×w$的小块，同时在$l_2$极线附近取若干小块，比较他们的差异。

比较的方法常见的有：

• SAD(sum of Absolute Difference)取两个小块的绝对值之和
• SSD(Sum of Squared Distance)取两个小块的差的平方和
• NCC(Normalized Cross Correlation)归一化互相关

$$S(A, B)_{N C C}=\frac{\sum_{i, j} A(i, j) B(i, j)}{\sqrt{\sum_{i, j} A(i, j)^{2} \sum_{i, j} B(i, j)^{2}}}$$

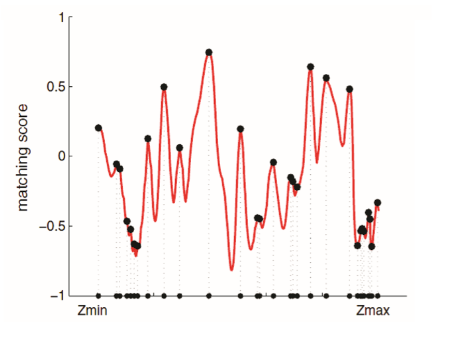
在搜索距离较长的情况下，我们通常会得到一个非凸函数：这个分布存在着许多峰值，然而真实的对应点必定只有一个。

1.2 高斯分布的深度滤波器

对深度的分布假设存在着若干种不同的做法。首先，在比较简单的假设条件下，我们 可以假设深度值服从高斯分布，得到一种类卡尔曼式的方法。

在上一节中，我们可以通过匹配求得一帧图片中特征点的大致位置和它的不确定度，现在需要做两件事：像素的不确定度和实际点深度的不确定度的关系？多帧图像的不确定度怎么融合？

融合的办法采用了高斯分布的计算性质：两个高斯分布的乘积依然是高斯分布。

假设某个点的深度服从$P(d)=N(\mu,\sigma^2)$，每当新的数据到来时，我们可以观测到它的深度，假设这个深度依然是高斯分布$P(d{obs})=N(\mu{obs},\sigma^2_{obs})$那么根据高斯分布的乘法公式可以得到：

$$\mu_{\text {fuse}}=\frac{\sigma_{\text {obs}}^{2} \mu+\sigma^{2} \mu_{\text {obs}}}{\sigma^{2}+\sigma_{\text {obs}}^{2}}, \quad \sigma_{\text {fuse}}^{2}=\frac{\sigma^{2} \sigma_{\text {obs}}^{2}}{\sigma^{2}+\sigma_{o b s}^{2}}$$

接下来考虑像素的不确定度和实际点深度的不确定度的关系，换句话说需要为上述式子$u{obs},\sigma^2{obs}$求值。

根据几何计算单个像素引起:

$$p'=t\frac{\sin{\beta'}}{sin{\gamma}}$$

如果认为极线搜索的块匹配仅有一个像素的误差，那么就可以设：

$$\sigma_{obs}=p-p'$$

在实际工程中，当不确定性小于一 定阈值之后，就可以认为深度数据已经收敛了。综上所述，我们给出了估计稠密深度的一个完整的过程：

1. 假设所有像素深度满足某个初始的高斯分布；
2. 当新数据产生时，通过极线搜索和块匹配确定投影点的位置；
3. 根据集合关系计算三角化后的深度以及不确定性；
4. 将当前观测融合进上一次的估计中。若收敛则停止计算，否则返回2。

2. RGB-D稠密建图

RGBD建图常见的是点云的方式。但是点云有几个明显的缺点：

• 点云地图通常规模很大.
• 点云地图产生了很多无用信息(比如地毯上的褶皱、阴暗处的影子)
• 点云地图无法处理运动物体。因为我们的做法里只有“添加点”，而没有“当点消失时把它移除”的做法。

因此可以采用改进的八叉树建图方法，这是一种灵活的、压缩的、又能随时更新的地图形式。

如果我 们把一个小方块的每个面平均切成两片，那么这个小方块就会变成同样大小的八个小方块。 这个步骤可以不断的重复，直到最后的方块大小达到建模的最高精度。在这个过程中，把 “将一个小方块分成同样大小的八个”这件事，看成“从一个节点展开成八个子节点”，那么，整个从最大空间细分到最小空间的过程，就是一棵八叉树（Octo-tree）。

当某个方块的所有子节点都被占据或都不被占据时，就没必要展开这个节点。例如，一开始地图为空白时，我们就只需一个 根节点，而不需要完整的树。当在地图中添加信息时，由于实际的物体经常连在一起，空白的地方也会常常连在一起，所以大多数八叉树节点都无需展开到叶子层面。所以说，八叉树比点云节省了大量的存储空间。

从点云层面来讲，我们自然可以用0 表示空白，1 表示被占据。这种 0-1 的表示可以用一个比特来存储，节省空间，不过显得有些过于简单了。由于噪声的影响，我们可能会看到某个点一会为 0，一会儿为 1；或者大部分时刻为 0，小部分时刻为 1；或者除了“是、否”两种情况之外，还有一个“未知” 的状态。我们会选择用概率形式表达某节点是否被占据的事情，例如用一个浮点数 [0-1] 来表达。如果不断观测到它被占据，那么让这个值不断增加；反之，如果不断观测到它是空白，那就让它不断减小即可。

为了避免增加超过1，我们采用对数变化性质：

$$y=logit(x)=log(\frac{x}{1-x})$$

可以看到，当 $y$ 从$−∞$ 变到 $+∞$ 时，$x$ 相应地从 0 变到了 1。而当 $y$ 取 0 时，$x$ 取 到 0.5。

假设我们在 RGB-D 图像中观测到某个像素带有深度 $d$，这说明了一件事：我们在深度值对应的空间点 上观察到了一个占据数据，并且，从相机光心出发，到这个点的线段上，应该是没有物体的（否则会被遮挡）。利用这个信息，可以很好地对八叉树地图进行更新，并且能处理运动的结构。