Sim3变换

Sim3变化比较难，主要用于SLAM回环检测匹配时的尺度校正。

1. 概述

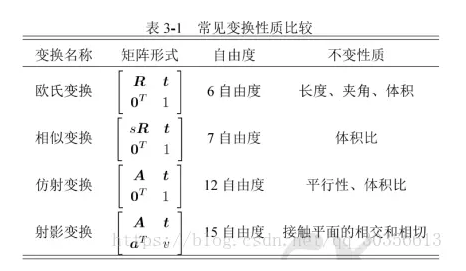
常见的欧式变换由6个自由度($R,T$各三个)，在SLAM问题中，可能会存在尺度的改变，因此自由度就变成了7个，见下图：

Sim3(Similarity Transformation)的提出就是为了解决两个坐标系之间的相似变换问题，只要我们能得到3对匹配好的点在两个坐标系下的坐标，我们就能解出相似变换。

从几何上理解：在欧式变换中，我们只需要两对匹配的点就可以求解，因为两个点构成向量，通过比较向量在两个空间的平移量和旋转量，就可以得到欧式变换的结果。而在相似变换中，通过增加一个点，三个点构成三角形，通过法向量能计算旋转量，通过面积相似性能计算尺度变化，利用$R,s$将两个面平行，通过计算面距离得到平移量。

从代数上理解：两组三维点，能构成6个方程，解6个未知数；三组三维点，构成9个方程，超定方程解7个未知数。

在SLAM中主要用于回环检测，因为回环过程中会产生尺度的漂移，需要计算当前帧和候选帧之间的sim3变换。

2. 算法

2.1 坐标系

假设3个点在左右两个坐标系下的坐标分别是$r{l,1},r{l,2},r{l,3}$和$r{r,1},r{r,2},r{r,3}$，令$r{l,1}$和$r{r,1}$分别为左右两个坐标系的原点，则我们可以算出这两个坐标系的$x,y,z$轴方向的单位向量：

$X$方向：$xl=r{l,2}-r_{l,1}$,则单位向量$\hat x_l=x_l/|x_l|$

$Y$方向：$yl=(r{l,3}-r{l,1})-[(r{l,3}-r_{l,1})·\hat x_l]\hat x_l$ ，则单位向量$\hat y_l=y_l/|y_l|$

上面式子中$(r{l,3}-r{l,1})·\hat xl$大小为$r{l,3}-r_{l,1}$在$x$轴的投影（没有方向），再乘以$\hat x_l$得到了方向。做差后得到了与$x$轴垂直的方向。

$Z$方向：$\hat z_l=\hat x_l \times \hat y_l$

根据所得的坐标系单位向量，可以得到左右两侧坐标系的各个方向单位向量构成的基底矩阵：

$$M_l=|\hat x_l \hat y_l \hat z_l| \\ M_r=|\hat x_r \hat y_r \hat z_r|$$

假设左边坐标系有一个向量 $r_l$ ,那么： $M_l^Tr_l$ 是 $r_l$ 在 $M_l$ 基底下的坐标，左乘 $M_r$ 变成右坐标系： $r_r=M_rM_l^Tr_l$变换为： $R=M_rM_l^T$

2.2 计算平移量

设有n个点，在左右坐标系中分别表示为 ${r{l,i}}$ 和 ${r{r,j}}$ ,我们的目的是找到如下的变换形式： $r_r=sR(r_l)+r_0$，其中$r_0$为平移偏移量。

实际当中，两个坐标系之间的变换不会那么容易计算出精确的变换向量，一般使用最小二乘法来求解。此时，这里的误差为：

$$e_i=r_{r,i}-sR(r_{l,i})-r_0$$

那么，求解的最小二乘问题变成了求解：

$$\sum^n_{i=1}\|e_i\|^2$$

首先计算左右两个坐标系所有点的质心：

$$r_l^-=\frac{1}{n}\sum^n_{i=1}r_{l,i}\\ r_r^-=\frac{1}{n}\sum^n_{i=1}r_{r,i}$$

则每一个点距离质心的距离为：

$$r_{l,i}'=r_{l,i}-r^-_l \\ r_{r,i}'=r_{r,i}-r^-_r\\ \sum_{i=1}^n r_{l,i}'=0 \\ \sum_{i=1}^nr_{r,i}'=0$$

由此得出：

$$\begin{eqnarray} &&r_{r,i}'=sR(r_{l,i}')-r_0' \\ &&\Longrightarrow r_0'=r_{r,i}'-sR(r_{l,i}')\\ &&\Longrightarrow r_0'=r_{r,i}'-sR(r_{l,i}-\overline r_l)\\ &&\Longrightarrow r_0'=r_{r,i}'-sR(r_{l,i})+sR(\overline r_l)\\ &&\Longrightarrow r_0'=r_0-r_r^-+sR(\overline r_l)\\ \end{eqnarray}$$

优化函数变为：

$$\begin{eqnarray} \sum_{i=1}^n\|e_i\|^2&&=\sum_{i=1}^n\|r_{r,i}'-[sR(r_{r,i}')+r_0'\|^2]\\ &&=\sum_{i=1}^n\|r_{r,i}'-sR(r_{l,i}')\|^2-2r_0'\cdot\sum_{i=1}^n[r_{r,i}'-sR(r_{l,i}')]+n\|r_0'\|^2 \end{eqnarray}$$

最后一项明显不为负，所以当最后一项等于0时最小，由此可以计算出平移量$t$：

$$\begin{eqnarray} t&&=r_0=r_r^--sR(r_l^-) \end{eqnarray}$$

2.3 尺度计算

旋转尺度不变性： $|R(r{l,i}’)|^2=|r{l,i}’|^2$ ，对误差式展开得：

$$\sum_{i=1}^n\|r'_{r,i}\|^2-2s\sum_{i=1}^nr'_{r,i} \cdot R(r'_{l,i})+s^2\sum\|r'_{l,i}\|^2$$

将上式写成：

$$S_r-2sD+s^2S_l$$

进一步拆分成：

$$(s\sqrt{S_l}-D/\sqrt{S_l})^2+(S_rS_l-D^2)/S_l$$

上面的式子只有第一项与s有关，所以当第一项等于0时达到最小，即 $s=D/S_l$ :

$$s=\sum_{i=1}^nr'_{r,i} \cdot R(r'_{l,i})/\sum_{i=1}^n\|r'_{l,i}\|^2$$

在误差模型中除一个根号s：

$$e_i=\frac{1}{\sqrt{s}}r’_{r,i}-\sqrt{s}R(r’_{i,j})$$

我们只是求误差的最小值，除以一个系数是没关系的，这样做的好处是最后求得的s与旋转因子无关，并且便于后面求解。

最后得到：

$$s=(\sum_{i=1}^n\|r'_{r,i}\|^2/\sum_{i=1}^n\|r'_{i=1}\|^2)^{1/2}$$

因此只有在D取得最大的情况下，误差才会最小，现在就把问题变为了求D的过程。

引入四元数qq表示旋转(具体推导见三维刚体运动那一部分)：

$$\sum_{i=1}^n r'_{r,i} \cdot R(r'_{l,i})= \sum_{i=1}^n(q'r'_{l,i}q'^*) \cdot r'_{r,i}=\sum_{i=1}^n(q'r'_{l,i}) \cdot (r'_{r,i}q')$$

左边等于：

$$q’r’_{l,i}=\left[\begin{matrix} 0 & -x’_{l,i} & -y’_{l,i} & -z’_{l,i}\\ x’_{l,i} & 0 & z’_{l,i} & -y’_{l,i} \\ y’_{l,i} & -z’_{l,i} & 0 & x’_{l,i} \\ z’_{l,i} & y’_{l,i} & -x’_{l,i} & 0 \end{matrix}\right]q’=R_{l,i}q’$$

右边等于：

$$r’_{r,i}q’=\left[\begin{matrix} 0 & -x’_{r,i} & -y’_{r,i} & -z’_{r,i}\\ x’_{r,i} & 0 & -z’_{r,i} & y’_{r,i} \\ y’_{r,i} & z’_{r,i} & 0 & -x’_{r,i} \\ z’_{r,i} & -y’_{r,i} & x’_{r,i} & 0 \end{matrix}\right]q’= R_{r,i}q’$$

所以又可以表达为：

$$\sum_{i=1}^n(R_{l,i}q') \cdot (R_{r,i}q')=\sum_{i=1}^nq'^TR_{l,i}^TR_{r,i}q'=q'^TNq'$$

为了求解$N$，先引入一个$M$矩阵：

$$M=\sum_{i=1}^nr'_{l,i}r'^T_{r,i}=\left[\begin{matrix} S_{xx} & S_{xy} & S_{xz}\\ S_{yx} & S_{yy} & S_{yz} \\ S_{zx} & S_{zy} & S_{zz} \end{matrix}\right]$$

则$N$矩阵就可以表示为:

$$N=\left[\begin{matrix} (S_{xx}+S_{yy}+S_{zz}) & S_{yz} -S_{zy} & S_{zx}-S_{xz} & S_{xy}-S_{yx}\\ S_{yz}-S_{zy} & (S_{xx}-S_{yy}-S_{zz}) & S_{xy}+S_{yx} & S_{zx}+S_{xz}\\ S_{zx}-S_{xz} & S_{xy}-S_{yx} & (-S_{xx}+S_{yy}-S_{zz}) & S_{yz}+S_{zy} \\ S_{xy} -S_{yx} & S_{zx}+S_{xz} & S_{yz}-S_{zy} &(-S_{xx}-S_{yy}+S_{zz}) \end{matrix}\right]$$

引出$M$来就是为了让其中的量来表示$N$，如上式。将$N$进行特征分解，求得最大特征值对应的特征向量为四元数表示的旋转。之后平移和尺度关系也能相应求解。