相机坐标系,世界坐标系,图像坐标系三者之间的转化关系在三维视觉中非常重要。本文介绍PNP和EPNP这两种办法用于关系转化的原理。
1. PNP算法
对极几何和单应矩阵都是解决2D-2D的问题,现在假设我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。
PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。它描述了当我们知道 n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。,如果两张图像中,其中一张特征点的 3D 位置已知,那么最少只需三个点对(需要至少一个额外点验证结果)就可以估计相机运动。
特征点的 3D 位置可以由 RGB-D 相机的深度图确定。因此,在双目或 RGB-D 的视觉里程计中, 我们可以直接使用 PnP 估计相机运动。
PnP估计方法有很多种,下面介绍P3P方法。
P3P还需要使用一对验证点,以从可能的解出选出正确的那一 个(类似于对极几何情形)。记验证点对为 D−d。
我们知道的是 A,B,C 在世界坐标系中的坐标,而不是在相机坐标系中的坐标。一旦 3D 点在相机坐标系 下的坐标能够算出,我们就得到了 3D-3D 的对应点,把 PnP 问题转换为了 ICP 问题。
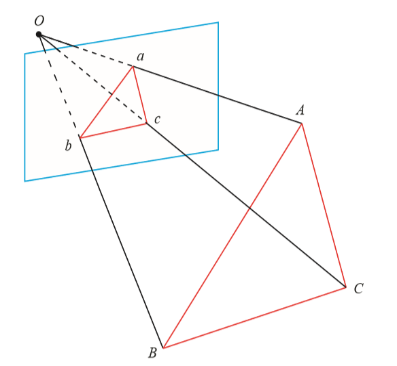
记$x=\dfrac{OA}{OC},y=\dfrac{OB}{OC}$,因为ABC在相机坐标系的位置未知,所以$x,y$也未知。另外记$u=\dfrac{BC^2}{AB^2},w=\dfrac{AC^2}{AB^2}$,由于ABC的世界坐标是已知的,所以$u,w$可以求出。通过转化可以得到:
由于我们知道了2D点在图像的位置,三个余弦角是已知的。该方程组是关于$x,y$的一个二元二次方程,最多可能得到四个解,因此在三个点之外还需要一组匹配点进行验证。
2. EPNP算法
PnP是利用已知匹配点对以及相机内参来求解相机位姿的算法,而EPnP则是针对$n≥3$情况下相机位姿求解的$O(n)$时间的算法。它描述了当我们知道 n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。
2.1 基本原理
上图表示场景中的平面π在两相机的成像,设平面π在第一个相机坐标系下的单位法向量为$N$,其到第一个相机中心(坐标原点)的距离为d,则平面π可以表示为:
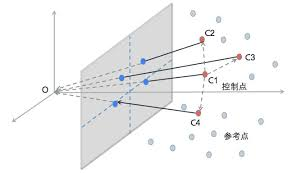
其中,世界坐标系中的点$p_i^w$可以表示为:
对于相机坐标系中的点$ p_i^c$,有:
对于上面的公式来说,首先需要说明的是$ \alpha _{ij}$确实存在,因为$c_j^w$构成的方程组是非正定的,所以一定存在解。理论上来说,控制点可以随便选择,这里选择控制点为参考点的中心,其他的点在主方向的单位长度处,从而提高算法的稳定性。
2.2 控制点在相机坐标系下的坐标
首先需要求解4个控制点在世界坐标系下的坐标,按照上述说法,就是找到点云的重心和点云的三个主方向,可以参考主成分分析PCA。
根据投影方程得到世界坐标系中参考点坐标和相机坐标系中参考点的约束关系:
写成矩阵的形式为:
将等式拆解,从第三行得到:
将$w_i$代入一二行,可以得到如下等式:
因此,可以得到如下线性方程组:
上面的方程中,四个控制点总共12个未知变量,$M$为$2n \times 12 $的矩阵。因此,x为矩阵M的右奇异向量,可以通过SVD得到。
$\beta$是分解得到的奇异值,个数为1-4个。
说明:使用$M^TM$比使用M计算量更小,因为$M^TM$的求解是常数复杂度,而$M$求逆是$O(n^3)$的复杂度,但是计算$M^TM$的复杂度是$O(n)$的。
2.3 计算R和t
通过前面的就算可以求出控制点在相机坐标系下的位置,下面就需要恢复出参考点在相机坐标系中的坐标。剩下的工作就是已知一组点云在两个坐标系中的坐标,求两个坐标系的位姿变换。
首先计算质心坐标:
然后计算去质心坐标:
之后计算矩阵:
最后进行SVD分解计算$R$和$T$: