本文围绕F基础矩阵、E本质矩阵、H单应矩阵这三个矩阵展开。

1. 对极几何原理

假设相机1运动到了相机2，两个相机的中心分别是$O_1,O_2$，成像得到了图像$I_1,I_2$。图像1中有一个特征点$p_1$，在图像2中对应了$p_2$（根据特征匹配的结果）。

也就是说通过两个图像的像素位置来估计相机的运动。

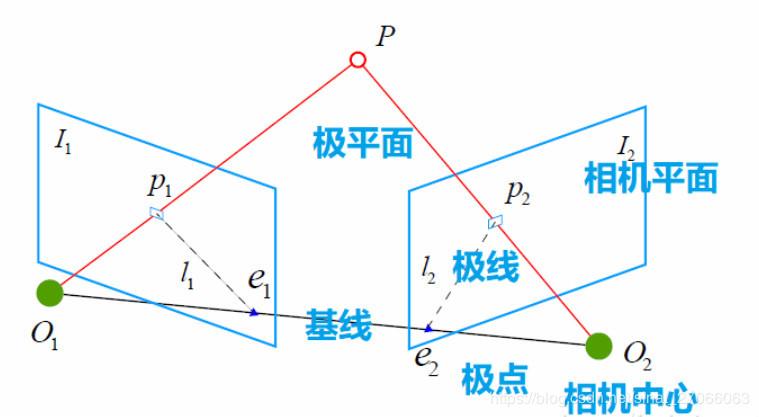
连线$\vec{O_1p_1}$和连线$\vec{O_1p_1}$在三维空间中交于点P，通过$O_1O_2P$这三个点可以形成一个平面，称之为极平面（Epipolar plane）,$O_1O_2$被称为基线(Baseline)，基线与图像平面的交点为$e_1e_2$记作极点(Epipoles)，$l_1l_2$称之为极线(Epipolar line)

假设第一个相机的P点的相机坐标系$P=[X,Y,Z]$。由于第一个相机的中心作为世界坐标系的原点，也就是说第一个相机没有旋转和平移，通过小孔相机模型可得：

从$p_1 = KP$可以得到$P=K^{-1}p_1$，带入第二个式子可以得到：

两边同时左乘$K^{-1}$，可以得到

假设$x_1=K^{-1}p_1,x_2=K^{-1}p_2$，尝试带入可得：

左右两边同时乘以反对称矩阵$t^{\land}$，由于$t^{\land}t=0$，所以：

两边再同时左乘$x_2^T$

由于$t^\land x_2$是向量$t$和向量$x_2$的叉积，得到的结果同时垂直于两向量，所以左边等于0，于是：

替换掉$x$:

这就是对极约束。令$F$来表示中间的基础矩阵：

由于相机内参已知，所以实际上我们可以用本质矩阵$E$来表示我们要求的对象：

2. 单应矩阵

单应(Homography)是射影几何中的概念，又称为射影变换。它把一个射影平面上的点(三维齐次矢量)映射到另一个射影平面上，并且把直线映射为直线。换句话说，单应是关于三维齐次矢量的一种线性变换，可以用一个3×3的非奇异矩阵$H$表示：

假设已经取得了两图像之间的单应，则可以通过单应矩阵H将两幅图关联起来：

假设使用同一相机在不同的位姿拍摄同一平面，如下图：

img

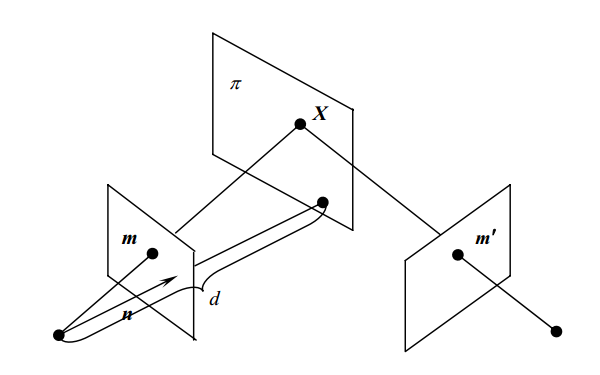
上图表示场景中的平面π在两相机的成像，设平面π在第一个相机坐标系下的单位法向量为$N$，其到第一个相机中心（坐标原点）的距离为$d$，则平面$π$可以表示为：

其中，$X_1$是三维点$P$在第一相机坐标系下的坐标，其在第二个相机坐标系下的坐标为$X_2$，

2.1 平移+旋转

假设，

将他们结合起来：

因此就得到了同一个平面两个不同坐标系的单应矩阵：

上述的单应矩阵在相机坐标系下，将它转化为像素坐标：

这个公式和对极几何非常像，本质上也是利用了对极几何的约束性质，基础矩阵的另一种表现形式。

2.2 只有旋转

由于没有平移，所以点在相机坐标系下的三维坐标没有变：

最后结果为：

在相机只有旋转而没有平移的情况下，两视图的对极约束就不再适用，这时可以使用单应矩阵$H$来描述两个图像像点的对应关系。

在这种情况下，不存在参数$d$，也就是说两图像点的匹配不依赖于三维点的深度信息，无法使用三角法重构出三维点在世界坐标系中的三维坐标。

3. 基础矩阵解法

3.1 八点法

考虑它的尺度等价性(按比例表示即可，不需要具体数值)，因此这个约束条件可以减少一个未知数，只需要8对匹配的点对就可以求解出两视图的基础矩阵$F$，这就是八点法

假设一对匹配的像点$p_1=[u_1,v_1,1]^T,p_2=[u_2,v_2,1]^T$，带入式子：

把基础矩阵F的各个元素当作一个向量处理:

就可以改写为：

求解上面的方程组就可以得到基础矩阵各个元素了。

求得本质矩阵$E$的解以后，需要得到$R$和$t$，这个过程使用奇异值分解(SVD)：

其中$U$和$V$都是正交矩阵，$\Sigma$为对角矩阵。解出来的结果有四种情况：

img

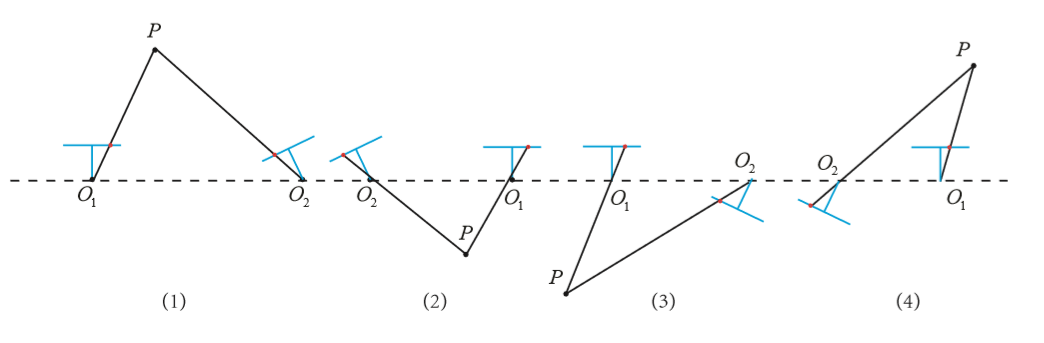
只有第一种解中，P 在两个相机中都具有正的深度。因此，只要把任意一点代入四种解中，检测该点在两个相机下的深度，就可以确定哪个解是正确的了。

3.2 RANSAC法

RANSAC做出了如下基本假设：

  1. 数据是由局内点组成，例如：数据的分布可以用一些模型参数来解释；
  2. 局外点是不能适应该模型的数据；
  3. 除此之外的数据属于噪声。

局外点产生的原因有：噪声的极值；错误的测量方法；对数据的错误假设。

一个简单的例子就是从一组观测数据中找出合适的二维直线。假设观测数据中包含局内点和局外点，其中局内点近似的被直线所通过，而局外点远离直线。

简单的最小二乘法不能找到适应于局内点的直线，原因是最小二乘法尽量去适应包括局外点在内的所有点。相反，RANSAC能得出一个仅仅利用局内点计算出模型，并且概率还足够高。但是，RANSAC并不能保证结果一定正确，为了保证算法有足够高的合理概率，我们必须小心的选择算法的参数。图示如下所示：

img

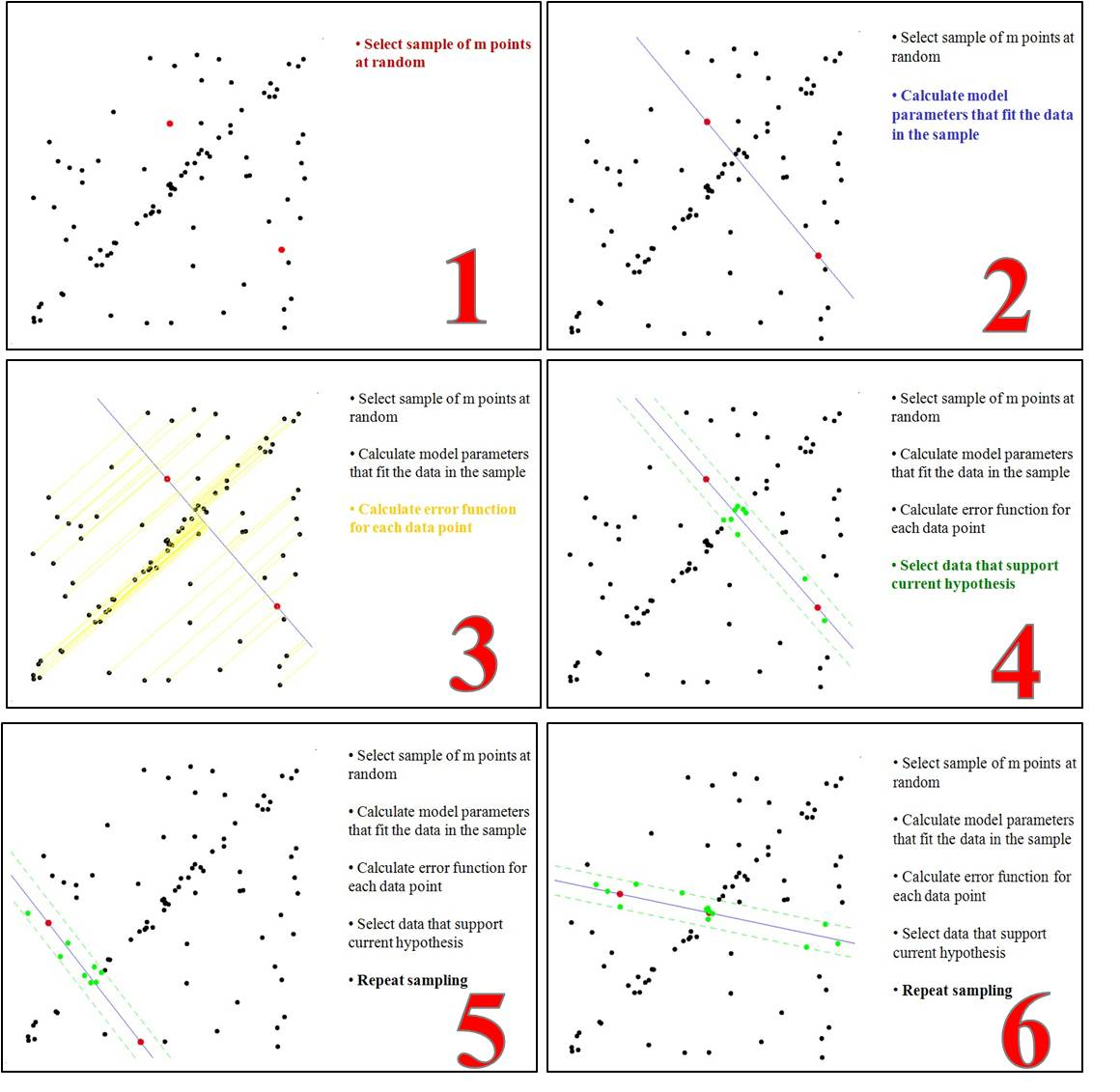
具体步骤如下：

  1. 有一个模型适应于假设的局内点，即所有的未知参数都能从假设的局内点计算得出；
  2. 用1中得到的模型去测试所有的其他数据，如果某个点适应于估计的模型，认为它也是局内点。
  3. 如果有足够多的点被归类于假设的局内点，那么估计的模型就足够合理；
  4. 然后，用所有假设的局内点去重新估计模型，因为它仅仅被初始的假设局内点估计过；
  5. 最后，通过估计局内点与模型的错误率来评估模型。

优缺点：

  • 优点：能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。
  • 缺点：计算参数的迭代次数没有上限，如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。

将RANSAC应用于基础矩阵的求解中，我们知道：

RANSAC算法从匹配数据集中随机抽取四个样本并保证这四个样本之间不共线。计算出单应性矩阵，然后利用这个模型测试所有数据，并计算满足这个模型数据点的个数和投影误差（即代价函数）若此模型为最优模型，则对应的代价函数最小：

结果如下：