本文详细介绍了SIFT特征检测的原理，以及相关的预备知识。

1. 概述

SIFT全称Scale Invariant Feature Transform，即尺度不变特征变换。相较于Harris和Fast这两种角点特征检测手段，SIFT专注于那些尺度不变的特征。

Harris算子不是尺度不变的，当图像变小时，检测结果的语义也会发生变化。

SIFT被设计出来的目的就是解决特征检测过程中经常遇到的尺度不变问题和旋转不变问题。

SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。

基本的算法流程是：

尺度空间极值点检测
关键点精确定位
确定方向
确定描述子

2. 高斯金字塔与高斯差分金字塔

高斯金字塔和高斯差分金字塔如下图所示：

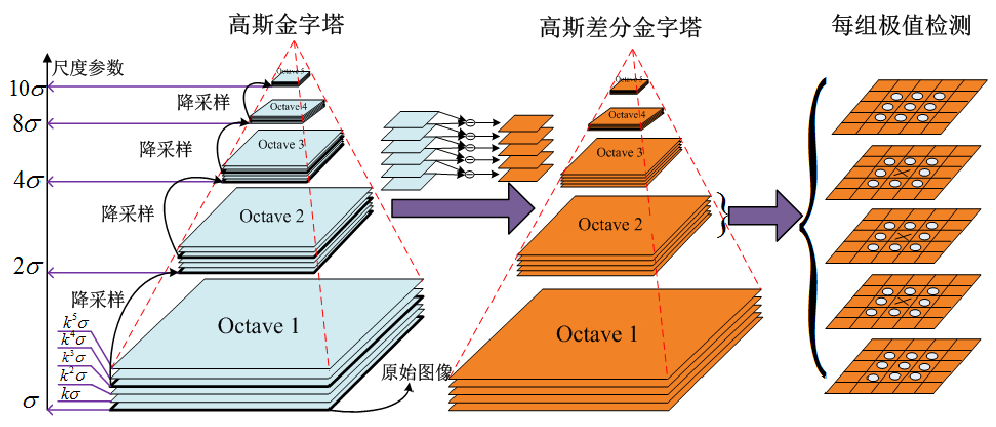
首先我们把输入的原图扩大一倍，由该图像进行高斯模糊的得到的第0组第0层图像设定为基准图像，设它的尺度为$\sigma_0$，称之为基准层尺度。则第0组第1层尺度为$k\sigma_0$，第0组第2层尺度为$k^2\sigma_0$，以此类推。

那么第0组中的图像的尺度为：

$\sigma = k^r\sigma_0 ,r=0,1,...,s-2$

第1组的第0层图像倒数第三张图像采样得到，若令$k=2^\frac{1}{s}$，则其相对于输入图像来说，尺度为$2\sigma_0$。

上述规律总结如下：

第$o$组第$r$层图像相对于输入图像的尺度为：

$\sigma = 2^ok^r\sigma_0\\ 其中，o = 0,1,2,...;r = 0,1,2,...,s+2$

该图像相对于本组中的基准图像的尺度为：

$\sigma = k^r\sigma_0$

而差分金字塔(DOG)就比较简单了，直接同组相邻的图像相减即可。

3. 算法流程

3.1 检测极值点

基本思路是在DOG金字塔中检测最大最小值点

具体检测思路是：

检测点和周围8个邻域点比较是否为极值点
检测点和尺度空间上下两层共计18个邻域点比较是否为极值点

同时满足这两个条件才可以被初步认定为特征点。

3.2 关键点精确定位

我们之前找到的极值点也就是离散空间中的极值点，但是离散空间中的极值点并不是真实的连续空间中的极值点。所以需要对DoG空间进行拟合处理，以找到极值点的精确位置和尺度。

我们得到的极值点是一个三维向量，包括它所在的尺度$\sigma$以及所在尺度图像中的位置坐标，即$X = (x,y,\sigma)$，泰勒展开即可得到

$f(\left[\begin{matrix}x\\y\\\sigma\end{matrix}\right]) \approx f(\left[\begin{matrix}x_0\\y_0\\\sigma_0\end{matrix}\right]) + [\frac{\partial f}{\partial x} \frac{\partial f}{\partial y} \frac{\partial f}{\partial \sigma}]\left(\left[\begin{matrix}x\\y\\\sigma\end{matrix}\right]-\left[\begin{matrix}x_0\\y_0\\\sigma_0\end{matrix}\right]\right) + \\\frac{1}{2}\left(\left[x \quad y \quad \sigma\right] - \left[x_0 \quad y_0 \quad \sigma_0\right]\right)\left[\begin{matrix}\frac{\partial^2 f}{\partial x \partial x} & \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial x \partial \sigma} \\ \frac{\partial^2 f}{\partial x \partial y}&\frac{\partial^2 f}{\partial y \partial y}&\frac{\partial^2 f}{\partial y \partial \sigma}\\ \frac{\partial^2 f}{\partial x \partial \sigma}&\frac{\partial^2 f}{\partial y \partial \sigma}&\frac{\partial^2 f}{\partial \sigma \partial \sigma}\end{matrix}\right]\left(\left[\begin{matrix}x\\y\\\sigma\end{matrix}\right]-\left[\begin{matrix}x_0\\y_0\\\sigma_0\end{matrix}\right]\right)$

若写成矢量形式，则为：

$f(X) = f(X_0）+\frac{\partial f^T}{\partial X}(X- X_0)+\frac{1}{2}(X-X_0)^T\frac{\partial^2 f}{\partial X^2}(X-X_0)$

此处，$X_0$表示中心，$X$表示拟合后连续空间的差值坐标，设$\hat{X} = X - X_0$表示偏移量。令导数为0则有：

$\hat{X} = -\frac{\partial^2 f^{-1}}{\partial X^2}\frac{\partial f}{\partial X}$

带入原公式：

$f(\hat{X}) = f(X_0) + \frac{1}{2}\frac{\partial f^T}{\partial X} \hat{X}$

若上式得到的偏移量大于阈值，则把位置移动到拟合后的新位置继续进行迭代求偏移量，若迭代过一定次数后偏移量仍然大于阈值，则抛弃该点。

有些极值点的位置是在图像的边缘位置的，因为图像的边缘点很难定位，同时也容易受到噪声的干扰，我们把这些点看做是不稳定的极值点，需要进行去除。

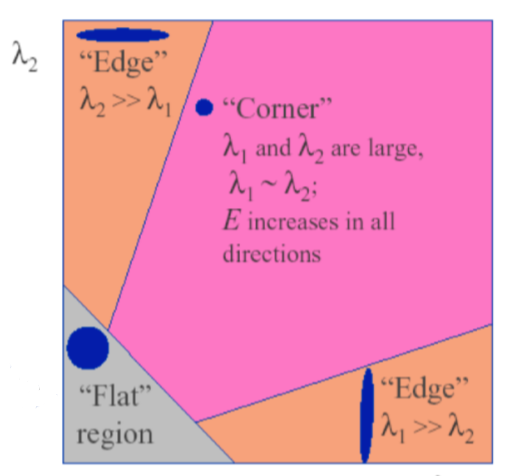
判定办法和Harris的办法很相似，设图像某点处的黑塞矩阵为

$M=\left[ \begin{matrix} I_x^2& I_xI_y \\ I_xI_y & I_y^2\end{matrix} \right] = \left[ \begin{matrix} A& C\\ C& B\end{matrix} \right]$

则有：

$detM=\lambda_1 \lambda_2=AB-C^2\\ traceM=\lambda_1 + \lambda_2 = A+B$

如果两个特征值相差特别大，就认为是边缘，排除。

3.3 方向计算

选取半径为$r$的区域作为邻域，计算每个像素的梯度幅角：

$\theta(x,y) = arctan\left(\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}\right)$

将 $2\pi$ 分为 $n$ 份，对应于直方图的 $n$ 个单位。比如分为6份，每个直方图代表 $60^o$：

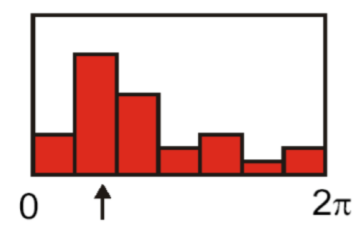
选取其中最高的一柱代表主方向。

之后将每个特征点的方向调整至一致，这期间一般使用双线性差值的办法填补像素。

3.4 确定描述子

步骤1：将$16\times16$区域作为一个patch，校正方向

步骤2：按照3.3所述的办法计算每个像素的方向和幅度

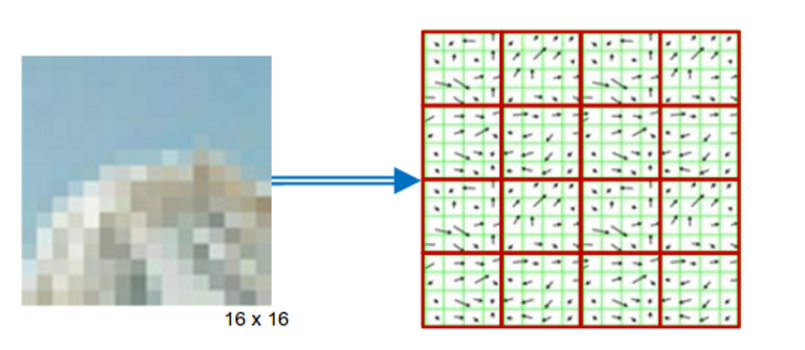
步骤3：将其分为$4\times4$的方框，计算每个方框的8方向直方图

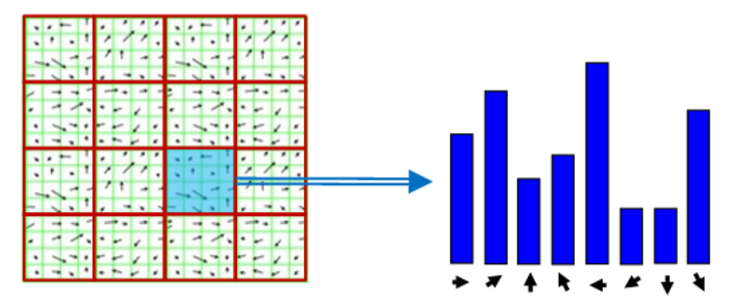
最后就能得到128维描述向量（每个柱可用1-8的数字表示）

SIFT特征检测