1. 首尾双指针
将两个指针分布在首尾,特别针对排序数组。

167 两数之和II-输入有序数组
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解答:
这道题在二分法那一篇中已经讲过了,现在我们改为用双指针。注意:使用双指针之前一定要确保排序。
vector<int> twoSum(vector<int>& numbers, int target) {
int l =0,r=numbers.size()-1;
if(numbers.size()==0) return vector<int>{-1,-1};
while(l<r)
{
if(numbers[l]+numbers[r]==target)
return vector<int>{l+1,r+1};
else if(numbers[l]+numbers[r]<target)
l++;
else
r--;
}
return vector<int>{-1,-1};
}
015 三数之和
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
解答:
这道题不太一样,它需要收集所有的可能结果,并且要排除重复结果。而且要注意它本身无序,所以要排序。
最简单的办法是利用std::set的去重特性来做,不要忘了if(nums[i]+nums[l]+nums[r]==0)也要做l++和r--,否则会死循环。
vector<vector<int>> threeSum(vector<int>& nums) {
set<vector<int>> s;
vector<vector<int>> res;
sort(nums.begin(),nums.end());
if (nums.size() < 2) return res;
for(int i=0;i<nums.size()-1;i++)
{
int l=i+1,r=nums.size()-1;
while(l<r)
{
if(nums[i]+nums[l]+nums[r]==0)
{
vector<int> tmp={nums[i],nums[l],nums[r]};
s.insert(tmp);
l++;r--;
}
else if(nums[i]+nums[l]+nums[r]<0) l++;
else r--;
}
}
for(auto x:s)
res.push_back(x);
return res;
}
上面这种办法慢得离谱,酌情使用。常规做法是去重。要注意对i去重是用过了再去,因为可能出现[-1,-1,2]这种情况,如果按照if(nums[i] == nums[i + 1]) continue;就会导致结果不全。
注意push进入结果时,l和r也需要增加或减少,不然会超时。
对
l和r去重时要注意,l++和r--用两次。- for去重时,应该要加入
i>0的判断,不然会溢出。 - 应该
nums[l]==nums[l+1]而不是nums[l-1]==nums[l]这样会和i重合
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<vector<int>> res;
if (nums.size() < 2) return res;
for (int i = 0; i < nums.size() - 2; i++)
{
//对i去重
if (i > 0 && nums[i] == nums[i - 1])
continue;
int l = i + 1, r = nums.size() - 1;
int sum = 0 - nums[i];
while (l < r)
{
if (nums[l] + nums[r] == sum)
{
res.push_back(vector<int>{nums[i], nums[l], nums[r]});
while (l < r && nums[l] == nums[l + 1]) l++;
while (l < r && nums[r] == nums[r - 1]) r--;
l++;
r--;
}
else if (nums[l] + nums[r] < sum)
{
while (l < r && nums[l] == nums[l + 1]) l++;
l++;
}
else
{
while (l < r && nums[r] == nums[r - 1]) r--;
r--;
}
}
}
return res;
}
016 最接近的三数之和
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
例如,给定数组 nums = [-1,2,1,-4], 和 target = 1.
与 target 最接近的三个数的和为2. (-1 + 2 + 1 = 2).
解答:
相较于上一题,不用去除重复。需要加一个closest,表示最接近的数。每次循环都比较更新维护这个数。要注意closet不能设为INT_MAX,后面可能会溢出。
int threeSumClosest(vector<int>& nums, int target) {
if (nums.size() < 3) return 0;
sort(nums.begin(),nums.end());
int closet = accumulate(nums.begin(),nums.begin()+3,0);
for(int i=0;i<nums.size()-2;i++)
{
int l=i+1,r=nums.size()-1;
while(l<r)
{
int sum=nums[l]+nums[r]+nums[i];
if(sum==target) return sum;
if(abs(sum-target)<abs(closet-target))
closet=sum;
else if(sum<target) l++;
else r--;
}
}
return closet;
}
018 四数之和
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
解答:
更015一样,多一层即可
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> res;
if(nums.size()<4) return res;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size()-3;i++)
{
if(i!=0&&nums[i]==nums[i-1]) continue;
for(int j=i+1;j<nums.size()-2;j++)
{
if(j!=i+1&&nums[j]==nums[j-1]) continue;
int l=j+1,r=nums.size()-1;
int sum12=nums[i]+nums[j];
while(l<r)
{
int sum34=nums[l]+nums[r];
if(sum12+sum34==target)
{
vector<int> tmp{nums[i],nums[j],nums[l],nums[r]};
res.push_back(tmp);
while(l<r&&nums[l]==nums[l+1]) l++;
while(l<r&&nums[r]==nums[r-1]) r--;
l++;
r--;
}
else if(sum12+sum34<target)
{
while(l<r&&nums[l]==nums[l+1]) l++;
l++;
}
else
{
while (l < r && nums[r] == nums[r - 1]) r--;
r--;
}
}
}
}
return res;
}
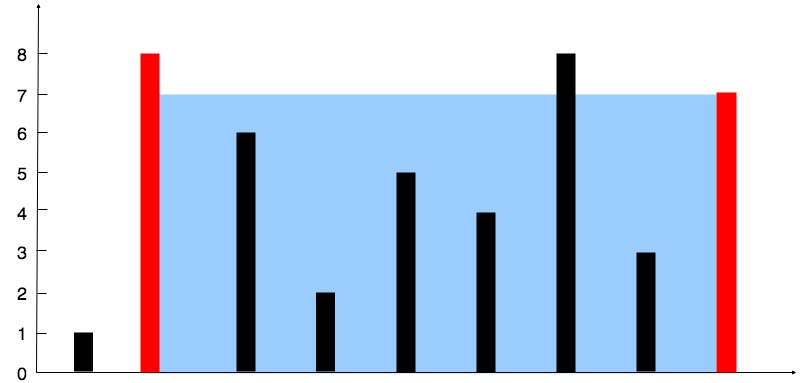
011 乘最多水的容器
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
解答:
面积=最短边*距离,要提高面积就有两种办法:增大最短边,保持长距离。让两边较小者往内移动,这样最有可能找到最大面积。同时,我们需要维护一个maxarea
int maxArea(vector<int>& height) {
int l=0,r=height.size()-1;
int maxarea = 0;
while(l<r)
{
int area = min(height[l],height[r])*(r-l);
maxarea=max(maxarea,area);
if(height[l]<height[r]) l++;
else r--;
}
return maxarea;
}
075 颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
解答:
典型的快排。采用了三指针,两个放首尾,index放中间。要保证index以前的都是有序的,我们构建两个标志zerotail和twohead分别表示最后一个0的下一个和第一个2的前一个,比如[0,1,1,2],zerotail=1,twohead=2。
注意:当nums[index] == 2交换时,index不能盲目前进,因为不知道被换过来的是1还是2,需要放到下一轮进行检验。(由于我们保证了index以前都是有序的,所以和0做交换是安全的)
注意:去重时,必须要判断twohead >= 0和zerotail < nums.size(),不然会溢出。比如[2],使得twohead=-1,下一次while就会导致nums[twohead]溢出。
注意:index小于等于twohead,要保证所有都检查完!
注意:while (zerotail < nums.size() && nums[zerotail] == 0)顺序很重要,不然会溢出!
void sortColors(vector<int>& nums) {
int zerotail = 0, twohead = nums.size() - 1;
while (zerotail < nums.size() && nums[zerotail] == 0) zerotail++;
while (twohead >= 0 && nums[twohead] == 2) twohead--;
int index = zerotail;
while (index <= twohead)
{
if (nums[index] == 0)
std::swap(nums[zerotail++], nums[index++]);
else if (nums[index] == 2)
std::swap(nums[twohead--], nums[index]);
else
index++;
}
}
2. 同向双指针
也可以称为滑动窗口法,使用滑动窗口时考虑三个问题:初始化窗口范围、终止条件、移动条件。
003 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
解答:
利用双指针l和r维护一个set,遇到不一样的就加进来,遇到一样的删尾巴。起始条件r=l=0,终止条件r==s.size()
当遇到重复时,并没有将前面的全部擦除,而是一个一个擦,这样很慢,但set没办法,它的迭代器不支持加减运算符。
int lengthOfLongestSubstring(string s) {
set<char> cache;
int l=0,r=0;
int maxlen=0;
while(r<s.size())
{
if(cache.find(s[r])==cache.end())
{
cache.insert(s[r++]);
maxlen=max(maxlen,r-l);
}
else
cache.erase(s[l++]);
}
return maxlen;
}
209 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组
解答:
注意右边的边界,一定要加双判断,不然要越界。是while (sum < s && right < len)不是if,所以可能会越界,不要搞晕了。
int minSubArrayLen(int s, vector<int>& nums) {
if (nums.empty())
return 0;
int left = 0, right = 0, sum = 0, len = nums.size();
int res = INT_MAX;
while (right < len)
{
while (sum < s && right < len)
sum += nums[right++];
while (sum >= s)
{
res = min(res, right - left);
sum -= nums[left++];
}
}
return res == INT_MAX ? 0 : res;
}
3. 其他双指针
028 实现strStr()
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
输入: haystack = "hello", needle = "ll"
输出: 2
解答:
这道题本质上应该用KMP算法,但一道easy级别的题目这么搞显然不合理。所以就用笨一点的分离双指针遍历好了。
两个指针,一个负责haystack搜索,找到合适的起始位置后,另一个也启动在needle和haystack一起搜索。
为空时,返回0,为了和C语言以及java中的API相对应。
int strStr(string haystack, string needle) {
if (needle == "") return 0;
int i = 0;
for (; i < haystack.size(); i++)
{
if (haystack[i] != needle[0]) continue;
int j = 0;
for (; j < needle.size(); j++)
{
if (haystack[i + j] != needle[j])
break;
}
if (j == needle.size()) return i;
}
return -1;
}
088 合并两个有序数组
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。初始化 nums1 和 nums2 的元素数量分别为 m 和 n。你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
解答:
从后往前遍历,维护三个指针:i负责nums1的有效位置,j负责nums2,index负责插入位置。
最后要把剩余的j补上去。
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i=m-1,j=n-1;
int len=nums1.size()-1;
while(i>=0&&j>=0)
{
if(nums1[i]>nums2[j])
nums1[len--]=nums1[i--];
else
nums1[len--]=nums2[j--];
}
while(j>=0) nums1[len--]=nums2[j--];
}