BFS和DFS是一对孪生兄弟,几乎所有DFS可以完成的地方BFS都可以完成。本章主要以BFS的介绍为主,DFS为辅。
1. 算法介绍
简单的说,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止。BFS同样属于盲目搜索。一般用队列数据结构来辅助实现BFS算法。
解题步骤一般是:
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。如果找到目标,则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
- 重复步骤2。
DFS递归和栈都能用,BFS统统使用队列。
2. 树的BFS
树BFS基本就是纯粹的模板,模板有两个while,第一个是大while,第二个是小while。假设如下的二叉树,最开始队列存储root,1
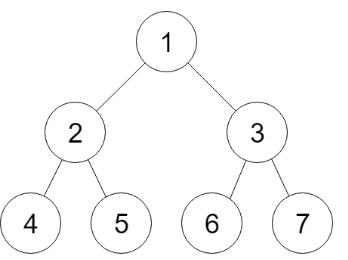
| while次数 | 队列存储结果 |
|---|---|
| 1 | [2,3] |
| 2 | [4,5,6,7] |
存储的顺序是正序还是反序,主要根据left和right的先后顺序。模板见102题。
102 二叉树的层次遍历
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)
3
/ \
9 20
/ \
15 7
RES=[[3],[9,20],[15,7]]
解答:
中序遍历用的是stack
注意要先判断是否为空,剩下的内容基本都是套路模板。注意while(!q.empty())是取非,不要马虎写错了。
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
vector<vector<int>> res;
if(root==NULL) return res;
q.push(root);
while(!q.empty())
{
auto size = q.size();
vector<int> tmp;
while(size--)
{
TreeNode* node = q.front();
q.pop();
tmp.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
res.push_back(tmp);
}
return res;
}
103 二叉树的锯齿形层次遍历
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
3
/ \
9 20
/ \
15 7
[[3],[20,9],[15,7]]
解答:
很巧妙的翻转。
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> res;
if(!root) return res;
queue<TreeNode*> q;
q.push(root);
int flag=0;
while(!q.empty())
{
vector<int> tmp;
auto size=q.size();
while(size--)
{
TreeNode* node=q.front();
tmp.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
q.pop();
}
if(flag%2==1) reverse(tmp.begin(),tmp.end());
flag++;
res.push_back(tmp);
}
return res;
}
107 二叉树的层次遍历 II
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
3
/ \
9 20
/ \
15 7
[[15,7],[9,20],[3]]
解答:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
//和102一样,最后反转即可
vector<vector<int>> res;
if (root == NULL)
return res;
queue<TreeNode*> myq;
myq.push(root);
while (!myq.empty())
{
vector<int> tmp;
auto size = myq.size();
while (size--)
{
TreeNode* node=myq.front();
myq.pop();
tmp.push_back(node->val);
if (node->left)
myq.push(node->left);
if (node->right)
myq.push(node->right);
}
res.push_back(tmp);
}
reverse(res.begin(), res.end());
return res;
}
104 二叉树的最大深度
给定一个二叉树,找出其最大深度。
3
/ \
9 20
/ \
15 7
返回它的最大深度 3
解答:
int maxDepth(TreeNode* root) {
if(root == NULL)
return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
int maxDepth(TreeNode* root) {
if(root == NULL)
return 0;
int num = 0;
queue<TreeNode *> que;
que.push(root);
while(!que.empty()){
int n = que.size();
for(int i = 0;i < n;++i){
TreeNode *cur = que.front();
if(cur->left != NULL)
que.push(cur->left);
if(cur->right != NULL)
que.push(cur->right);
que.pop();
}
num++;
}
return num;
}
110 平衡二叉树
判断一个二叉树是否平衡,即一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
解答:
bool isBalanced(TreeNode* root) {
return dfs(root)==-1?false:true;
}
int dfs(TreeNode* root){
if(root==NULL)
return 0;
int left=dfs(root->left);
int right=dfs(root->right);
if(abs(left-right)>1) return -1;
return max(left,right)+1;
}
111 二叉树的最小深度
解答:
int minDepth(TreeNode* root) {
if(root == NULL)
return 0;
int num = 0;
queue<TreeNode *> que;
que.push(root);
while(!que.empty()){
int n = que.size();
for(int i = 0;i < n;++i){
TreeNode *cur = que.front();
if(cur->left != NULL)
que.push(cur->left);
if(cur->right != NULL)
que.push(cur->right);
que.pop();
}
num++;
if(pow(2,num-1)!=n) return num-1;
}
return num;
}
116 填充每个节点的下一个右侧节点指针
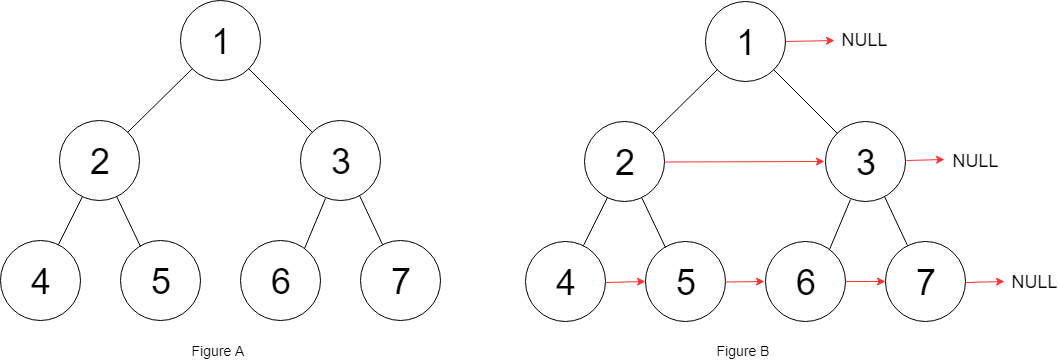
解答:
Node* connect(Node* root) {
if (!root) return NULL;
queue<Node*> q;
q.push(root);
//每一个while循环都是一层
//size就是这一层的节点数量
//i<size-1时,代表要右指
//每一层干三件事:1.弹出旧的 2.判断右指 3.添加新的
while (!q.empty()) {
auto size = q.size();
for (int i = 0; i < size; ++i) {
Node* t = q.front(); q.pop();
if (i < size - 1) {
t->next = q.front();
}
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
}
return root;
}
199 二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
解答:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
if (!root)
return res;
queue<TreeNode*> q;
q.push(root);
while (!q.empty())
{
int size = q.size();
res.push_back(q.front()->val);
//BFS新技术size法
while (size--)
{
TreeNode* tmp = q.front();
q.pop();
if (tmp->right)
q.push(tmp->right);
if (tmp->left)
q.push(tmp->left);
}
}
return res;
}
226 翻转二叉树
4
/ \
2 7
/ \ / \
1 3 6 9
4
/ \
7 2
/ \ / \
9 6 3 1
解答:
TreeNode* invertTree(TreeNode* root) {
if(root==NULL) return NULL;
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
auto size = q.size();
while(size--)
{
TreeNode* node = q.front();
q.pop();
swap(node->left,node->right);
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
return root;
}
2. 图的BFS
133 克隆图
给定无向连通图中一个节点的引用,返回该图的深拷贝(克隆)。图中的每个节点都包含它的值 val(Int) 和其邻居的列表(list[Node])。
解答:
需要通过map来进行映射,记录是否已经拷贝。
记住:nei是原节点,m[nei]是复制节点,凡是m[xx]都是复制节点
Node* cloneGraph(Node* node) {
if (!node) return NULL;
map<Node*, Node*> m;
queue<Node*> q;
q.push(node);
//注意下vector<Node*>{}写法
Node* clone = new Node(node->val, vector<Node*>{});
m[node] = clone;
while (!q.empty())
{
Node* t = q.front();
q.pop();
for (Node* nei : t->neighbors)
{
//nei是原节点,m[nei]是复制节点,凡是
//m[xx]都是复制节点
if (!m.count(nei))
{
m[nei] = new Node(nei->val,vector<Node*>{});
q.push(nei);
}
m[t]->neighbors.push_back(m[nei]);
}
}
return clone;
}
207 课程表
现在你总共有 n 门课需要选,记为 0 到 n-1。在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;
并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
解答:
本质就是有向图是否存在环的问题。
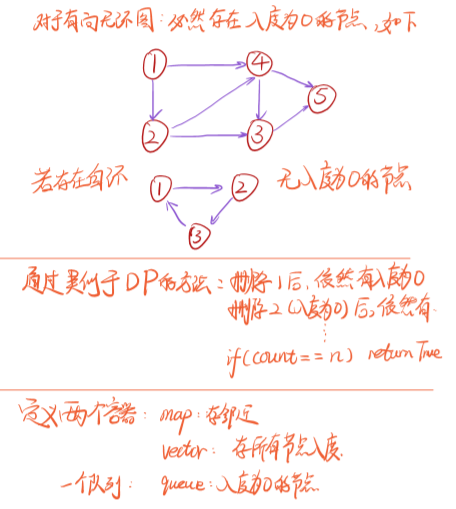
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
//有向图的标准设置:map<int, set<int>>存领域,vector<int>存入度
map<int, set<int>> adjacent;
vector<int> indegree(numCourses);
for (auto& edge : prerequisites) //建图
{
int from = edge[0];
int to = edge[1];
adjacent[from].insert(to);
indegree[to]++;
}
int count = 0;
queue<int> Inq;
for (int i = 0; i < numCourses; i++)
if (!indegree[i])
Inq.push(i);
while (!Inq.empty())
{
auto v = Inq.front();
Inq.pop();
count++;
auto adjs = adjacent[v];
//因为把v删了,所以入度也要改变
for (auto& adj : adjs)
{
indegree[adj]--;
if (!indegree[adj])
Inq.push(adj);
}
}
//reverse(indegree.begin(), indegree.end());;
return count == numCourses;
}
210 课程表 II
和上面一样,不过要记录下可能的课程顺序(一种即可)
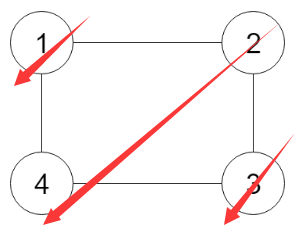
输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
解答:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> res;
map<int, set<int>> adjacent;
vector<int> indegree(numCourses);
for (auto& edge : prerequisites)
{
int from = edge[0];
int to = edge[1];
adjacent[from].insert(to);
indegree[to]++;
}
int count = 0;
queue<int> Inq;
for (int i = 0; i < numCourses; i++)
if (!indegree[i])
Inq.push(i);
while (!Inq.empty())
{
auto v = Inq.front();
Inq.pop();
count++;
//添加
res.push_back(v);
auto adjs = adjacent[v];
//因为把v删了,所以入度也要改变
for (auto& adj : adjs)
{
indegree[adj]--;
if (!indegree[adj])
Inq.push(adj);
}
}
//修改
if (numCourses != count)
return vector<int>{};
else
{
reverse(res.begin(), res.end());
return res;
}
}
3. 其他结构的BFS和DFS
079 单词搜索
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
board =
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
解答:
bool exist(vector<vector<char>>& board, string word) {
if (board.empty() || word.empty()){
return false;
}
int row = board.size(), col = board[0].size();
vector<vector<int>> f(row, vector<int>(col, 0));
for (int i = 0; i < row; ++i){
for (int j = 0; j < col; ++j){
if (dfs(board, word, 0, i,j, f)){
return true;
}
}
}
return false;
}
bool dfs (vector<vector<char>>& board, string& word,
int size, int x, int y, vector<vector<int>>& f){
if (size == word.size()){
return true;
}//outofbound
if (x < 0 || x >= board.size()
|| y < 0 || y > board[0].size()
|| board[x][y] != word[size]){
return false;
}
if (f[x][y] == 0) {
f[x][y] = 1;
if (dfs(board, word, size+1, x+1, y, f)
|| dfs(board, word, size+1, x-1, y, f)
|| dfs(board, word, size+1, x, y+1, f)
|| dfs(board, word, size+1, x, y-1, f)){
return true;
}
f[x][y] = 0;
}
return false;
}
101 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
bool isSymmetric(TreeNode* root) {
return isMirror(root,root);
}
bool isMirror(TreeNode* p,TreeNode* q){
if(!p&&!q) return true;
if(!p||!q) return false;
if(p->val==q->val)
return isMirror(p->left,q->right)&&isMirror(p->right,q->left);
return false;
}
108 将有序数组转化为二叉树
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
解答:
注意区间的开闭,root->left=dfs(nums,l,mid);以及root->right=dfs(nums,mid+1,r);
TreeNode* sortedArrayToBST(vector<int>& nums) {
int len = nums.size();
return dfs(nums,0,len);
}
TreeNode* dfs(vector<int>& nums,int l,int r){
if(l==r) return NULL;
int mid=(l+r)/2;
TreeNode* root=new TreeNode(nums[mid]);
root->left=dfs(nums,l,mid);
root->right=dfs(nums,mid+1,r);
return root;
}
127 单词接龙
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
- 每次转换只能改变一个字母
- 转换过程中的中间单词必须是字典中的单词。
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
返回它的长度 5。
解答:
实质上就是统计BFS的层数

int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
if (wordList.size() == 0)
return 0;
//假如当前为dot,
//则下一个为log或dog,q就是存log和cog的
queue<string> q;
//字典,存单词
map<string, int> dic;
//初始化字典,1表示有这个单词
for (int i = 0; i < wordList.size(); i++)
dic[wordList[i]] = 1;
q.push(beginWord);
int layer=1;
dic.erase(beginWord); //及时擦去,避免自环
while ((!q.empty()) && dic.size())
{
//取一个出来
auto size=q.size();
layer++;
while(size--)
{
string now = q.front();
q.pop();
for (int i = 0; i < now.size(); i++)
{
string tmp = now;
for (char c = 'a'; c <= 'z'; c++)
{
if (tmp[i] == c) continue;
else tmp[i] = c;
if (dic.find(tmp) != dic.end())
{
if (tmp == endWord)return layer;
q.push(tmp);
dic.erase(tmp); //擦掉tmp不是now
}
}
}
}
}
return 0;
}
200 岛屿数量
给定一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
11000
11000
00100
00011
输出: 3
解答:
绝对不能用size法,因为grid是变化的。
//总体思路是把某个点1相连通的区域变为0,
//这样有多少个点就有多少个连通
//BFS用队列,DFS使用递归
int numIslands(vector<vector<char>>& grid) {
if (grid.size() == 0 || grid[0].size() == 0) return 0;
const int M = grid.size(), N = grid[0].size();
int res = 0;
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (grid[i][j] == '1') {
++res;
dfs(grid, i, j);
}
}
}
return res;
}
// gird[x][y] = 1, delete it and its around.
void dfs(vector<vector<char>>& grid, int x, int y) {
const int M = grid.size(), N = grid[0].size();
queue<pair<int, int>> q;
q.push({ x, y });
while (!q.empty()) {
auto head = q.front(); q.pop();
int x = head.first;
int y = head.second;
if (grid[x][y] != '1') continue;
grid[x][y] = '0';
for (auto d : dirs) {
int i = x + d.first;
int j = y + d.second;
if (i < 0 || i >= M || j < 0 || j >= N || grid[i][j] != '1') {
continue;
}
q.push({ i, j });
}
}
}