介绍Leetcode中的一些数学题,按反转、进位、进制等问题分类。
1. 数字反转
007 整数反转
给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
输入: -123
输出: -321
输入: 120
输出: 21
解答:
可以转化为字符串来做,也可以按照数学题中常见的数字分割来做。注意检查溢出。不能写x!=0,这样负数就无效了。
int reverse(int x) {
long sum=0;
while(x)
{
sum=sum*10+x%10;
x=x/10;
}
if(sum>INT_MAX||sum<INT_MIN)
return 0;
else
return sum;
}
009 回文数
判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
输入: 121
输出: true
输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
解答:
bool isPalindrome(int x) {
if(x<0) return false;
long sum=0;
int origin=x;
while(x)
{
sum=sum*10+x%10;
x=x/10;
}
return (sum==origin)?true:false;
}
2. 进位问题
043 字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
输入: num1 = "2", num2 = "3"
输出: "6"
输入: num1 = "123", num2 = "456"
输出: "56088"
解答:
注意index = num1.size() + num2.size() - 2;因为是数组下标。进位最后不要忘了carry还要加上去。
/*
* 1 2 3
* * 3 2 1
* ----------
* 1 2 3
* 2 4 6
* 3 6 9
* --------------
* 3 8 14 8 9
* 乘法的计算是错位相加最后的位数=n+(m-1),原数有3位,乘以一个三位数相当于向左添加了2位
* */
string multiply(string num1, string num2) {
if (num1 == "0" || num2 == "0") return "0";
vector<int> res(222, 0);
int index = num1.size() + num2.size() - 2;
for (int i = num1.size() - 1; i >= 0; i--)
{
for (int j = num2.size() - 1; j >= 0; j--)
{
int mul = (num1[i] - '0') * (num2[j] - '0');
int t = index - i - j; //index:0-4
res[t] = res[t] + mul;
}
}
//处理完成3 8 14 8 9
//反过来装 9 8 14 8 3
string str = "";
int carry = 0;
//注意这里是等于!!
for (int i = 0; i <= index; i++)
{
res[i] += carry;
carry = 0;
if (res[i] >= 10)
{
carry = res[i] / 10;
res[i] = res[i] % 10;
}
str.append(to_string(res[i]));//数字转string
}
if (carry != 0) str.append(to_string(carry));
reverse(str.begin(), str.end());
return str;
}
066 加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外,这个整数不会以零开头。
输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
解答:
分三种情况讨论即可。
vector<int> plusOne(vector<int>& digits) {
int len = digits.size();
int lastdigit = digits[len-1];
if(lastdigit!=9)
{digits[len-1]+=1; return digits;}
int flag=0;
for(auto x:digits)
if(x==9) flag++;
if(flag==len)
{
vector<int> res(len+1,0);
res[0]=1;
return res;
}
int carry = 0;
digits[len-1]+=1;
for(int i=len-1;i>=0;i--)
{
digits[i]+=carry;
carry=0;
if(digits[i]>=10)
{
carry = digits[i]/10;
digits[i]=digits[i]%10;
}
}
return digits;
}
067 二进制求和
给定两个二进制字符串,返回他们的和(用二进制表示)。输入为非空字符串且只包含数字 1 和 0。
输入: a = "1010", b = "1011"
输出: "10101"
解答:
注意判空。
string addBinary(string a, string b) {
string res;
int carry=0;
while(!a.empty()||!b.empty())
{
int sum=0;
sum+=carry;
carry=0;
if(!a.empty())
{
sum+=a.back()-'0';
a.pop_back();
}
if(!b.empty())
{
sum+=b.back()-'0';
b.pop_back();
}
carry=sum/2;
res.append(to_string(sum%2));
}
if(carry!=0) res.append(to_string(carry));
reverse(res.begin(),res.end());
return res;
}
3. 进制
168 Excel表列名称
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...
解答:
string convertToTitle(int n) {
if (n <= 0)
return "";
string res;
while (n > 0)
{
//假设26,取余后变为1了,结果不正确
//不能(n%26)-1+'A'
n--;
res=char((n % 26) + 'A')+res;
n = n / 26;
}
return res;
}
171 Excel表列序号
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
解答:
int titleToNumber(string s) {
int sum=0;
for(auto c:s)
{
int val = c-'A'+1;
sum=sum*26+val;
}
return sum;
}
4. 其他
029 两数相除
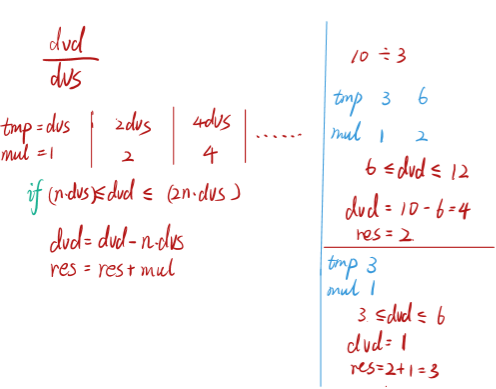
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数 divisor 得到的商。
输入: dividend = 10, divisor = 3
输出: 3
输入: dividend = 7, divisor = -3
输出: -2
解答:
int divide(int dividend, int divisor) {
long ans = 0, up = std::fabs(dividend), down = std::fabs(divisor);
while(up >= down){
long count = 1, base = down;
while(up > (base << 1)){
count <<= 1;
base <<= 1;
}
ans += count;
up -= base;
}
ans = ((dividend < 0)^(divisor < 0)) ? -ans : ans;
return (ans > INT_MAX || ans < INT_MIN) ? INT_MAX : ans;
}
050 Pow(x,n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
解答:
如果直接线性循环,太慢通不过。需要用快速幂算法,复杂度O(lgn)
double myPow(double x, int n) {
//排除特殊情况
if (n == 0) return 1;
//一定要转化为long型,防止表示-n时溢出
long long tmpn=n;
if (n < 0)
{
x = 1 / x;
tmpn=-(long long)n;;
}
return mymypow(x, tmpn);
}
double mymypow(double x, long long n)
{
//递归出口
if (n == 1) return x;
//递归主体
long long tmp = n / 2;
double res = mymypow(x, tmp);
//返回情况
if (n % 2 == 0) return res * res;
else return res * res * x;
}
172 阶乘后的零
给定一个整数 n,返回 n! 结果尾数中零的数量。
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
解答:
首先题目的意思是末尾有几个0,
比如$6! = [1 2 3 4 5 6]$其中只有25末尾才有0,所以就可以抛去其他数据专门看2和5 以及其倍数,毕竟 4 * 25末尾也是0
比如$10!= [2456810]$其中 $4$能拆成$22$ ,$10$能拆成$25$ 所以$10! = [2(22)5(23)(222)(2*5)]$一个2和一个5配对 就产生一个0 所以10!末尾2个0
转头一想 2肯定比5多 所以只数5的个数就行了
假若N=31 31里能凑10的5为$[5, 25, 35, 45, 25, 65]$, 其中 25还能拆为 5*2
int trailingZeroes(int n) {
int count = 0;
while(n/5!=0){
count+=n/5;
n/=5;
}
204 计数质数
统计所有小于非负整数 n 的质数的数量。
输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
解答:
如果x是质数,则nx全部都不是质数
int countPrimes(int n) {
if (n < 2)
return 0;
int count = 0;
vector<bool> judge(n, true);
for (int i = 2; i < n; i++)
{
if (judge[i])//如果是质数
{
for (int j = i * 2; j < n; j = j + i)
{
judge[j] = false;
}
count++;
}
}
return count;
}