由于C语言的缺陷，Redis自身创建了许多有用的数据结构，包括：简单动态字符串、链表、字典、跳跃表、整数集合、压缩列表。

1. 简单动态字符串

传统C语言的字符串以空字符结尾，而Redis自己重新构建了一种新的字符串结构，命名为简单动态字符串(simple dynamic string, SDS)。

在Redis中，C字符串只会用在一些无须修改的地方，比如打印常量：

redisLog(REDIS_WARNING,"Redis is now ready to exit, bye bye...");

如果是需要修改的地方，会使用SDS来表示：

redis> RPUSH fruits "apple" "banana" "cherry"
(integer) 3

Redis 将在数据库中创建一个新的键值对，其中：

key是一个字符串对象，底层保存了一个字符串fruits的SDS。
value是一个列表对象，列表包含了三个字符串对象，由SDS实现。

1.1 SDS的定义

SDS是一个结构体，定义在sds.h/sdshdr中

struct sdshdr {
    // 记录 buf 数组中已使用字节的数量
    // 等于 SDS 所保存字符串的长度
    int len;
    // 记录 buf 数组中未使用字节的数量
    int free;
    // 字节数组，用于保存字符串
    char buf[];
};

下面给出了一个示例，free为0代表所有空间都被使用，len长度为5，表示SDS保存的字符串长度为5，buf就是字符串实体。

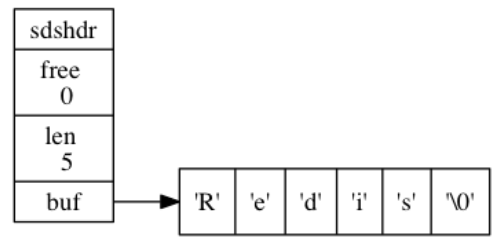
保存空字符的1字节空间不计算在len属性内。遵循空字符结尾这一惯例的好处是， SDS 可以直接重用一部分 C 字符串函数库里面的函数。

比如我们不需要对SDS专门设置打印函数。

printf("%s",s->buf);

1.2 SDS 与 C 字符串的区别

C 语言使用的简单的字符串表示方式，并不能满足 Redis 对字符串在安全性、效率、以及功能方面的要求。主要有以下几个弊端。

（1）C字符串获取长度的能力有限

C字符串需要依靠遍历获取长度，时间复杂度$O(N)$，而SDS本身记录了len，所以时间复杂度$O (1)$，常数时间。

（2）杜绝缓冲区溢出

由于C字符串不记录长度，当我们拼接两个字符串的时候，容器可能因为空间不足发生溢出。redis中的sdscat将在执行拼接操作前检查长度是否充足，若不足则先拓展空间，再拼接。

（3）减少修改字符串时带来的内存重分配次数

C字符串类似于数组，每次修改大小都会重新分配以此内存。Redis的分配原理类似于std::vector，通过空间预分配的办法优化字符串增加，分配规则如下：

若len比较小（小于1MB），则free是len一样大。如果修改后len为13字节，则free也为13字节，buf实际长度为13+13+1=27字节。
若len比较大（大于1MB），则每次free只会有1MB，比如修改后len为30MB，则free为1MB，总长度为30MB+1MB+1byte。

此外，使用惰性空间释放来优化字符串缩短。当缩短时，将释放的空间放入free中保存起来，等待使用。

（4）二进制安全

C字符串以空字符\0结尾，使得 C 字符串只能保存文本数据，而不能保存像图片、音频、视频、压缩文件这样的二进制数据。我们希望有一种使用空字符来分割多个单词的特殊数据格式。换句话说，数据写入时什么样，读取时就是什么样。

SDS利用len来判断是否结束，而不是空字符\0

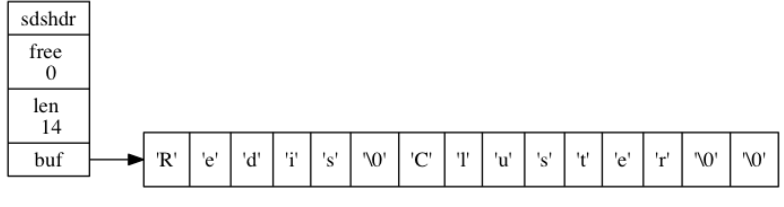
2. 链表

链表随机读写能力差，但增删和重排能力较强。C语言没有链表结构，所以Redis自制了一个。

链表节点定义在adlist.h/listNode，如下：

typedef struct listNode {
    // 前置节点
    struct listNode *prev;
    // 后置节点
    struct listNode *next;
    // 节点的值
    void *value;
} listNode;

这是一个双端链表。

虽然可以多个Node组成链表，但是为了方便，Redis设计了adlist.h/list 来持有链表。

typedef struct list {
    // 表头节点
    listNode *head;
    // 表尾节点
    listNode *tail;
    // 链表所包含的节点数量
    unsigned long len;
    // 节点值复制函数
    void *(*dup)(void *ptr);
    // 节点值释放函数
    void (*free)(void *ptr);
    // 节点值对比函数
    int (*match)(void *ptr, void *key);
} list;

Redis 的链表实现的特性可以总结如下：

双端
无环，表头和结尾都指向NULL
带有表头表位指针，访问$ O (1)$
自带链表长度计数器
多态：使用void*来保存节点值，有泛型编程内味了。

3. 字典

在字典中，一个键（key）可以和一个值（value）进行关联（或者说将键映射为值），这些关联的键和值就被称为键值对。字典中的每个键必须保证都是独一无二的。C并没有这样的结构，所以Redis自己实现了。

3.1 字典的实现

Redis 字典所使用的哈希表由 dict.h/dictht 结构定义：

typedef struct dictht {
    // 哈希表数组
    dictEntry **table;
    // 哈希表大小
    unsigned long size;
    // 哈希表大小掩码，用于计算索引值
    // 总是等于 size - 1
    unsigned long sizemask
    // 该哈希表已有节点的数量
    unsigned long used;
} dictht;

table 是一个数组，数组中的每个元素都是一个指向 dict.h/dictEntry 结构的指针。

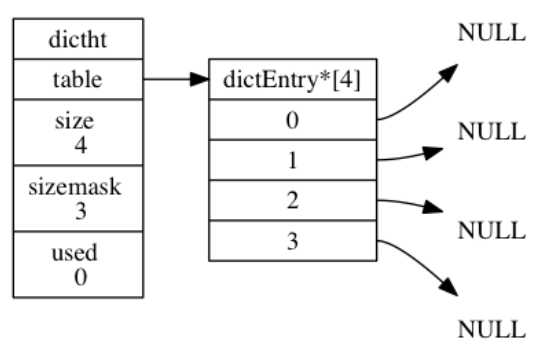
哈希表节点使用 dictEntry 结构表示，每个 dictEntry 结构都保存着一个键值对：

typedef struct dictEntry {
    // 键
    void *key;
    // 值
    union {
        void *val;
        uint64_t u64;
        int64_t s64;
    } v;
    // 指向下个哈希表节点，形成链表
    struct dictEntry *next;
} dictEntry;

v 属性则保存着键值对中的值，值可以是一个指针，或者是一个 uint64_t 整数，又或者是一个 int64_t 整数。

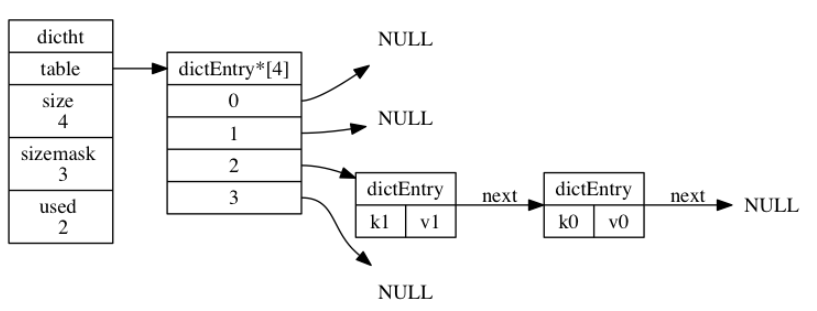
next 属性是指向另一个哈希表节点的指针，这个指针可以将多个哈希值相同的键值对连接在一次，以此来解决键冲突（collision）的问题。

下图中，键的索引值都是2，通过链表的形式完成了冲突的规避。

上面提到的是哈希表和哈希表节点的实现，现在来说真正的字典结构。Redis 中的字典由 dict.h/dict 结构表示：

typedef struct dict {
    // 类型特定函数
    dictType *type;
    // 私有数据
    void *privdata;
    // 哈希表
    dictht ht[2];
    // rehash 索引
    // 当 rehash 不在进行时，值为 -1
    int rehashidx; /* rehashing not in progress if rehashidx == -1 */
} dict;

其中type 属性和 privdata 属性是针对不同类型的键值对，为创建多态字典而设置的。

type 属性是一个指向 dictType 结构的指针，每个 dictType 结构保存了一簇用于操作特定类型键值对的函数。
privdata 属性则保存了需要传给那些类型特定函数的可选参数。

typedef struct dictType {
    // 计算哈希值的函数
    unsigned int (*hashFunction)(const void *key);
    // 复制键的函数
    void *(*keyDup)(void *privdata, const void *key);
    // 复制值的函数
    void *(*valDup)(void *privdata, const void *obj);
    // 对比键的函数
    int (*keyCompare)(void *privdata, const void *key1, const void *key2);
    // 销毁键的函数
    void (*keyDestructor)(void *privdata, void *key);
    // 销毁值的函数
    void (*valDestructor)(void *privdata, void *obj);
} dictType;

哈希表数组ht包含了两个元素，一般情况下，字典只使用 ht[0] 哈希表， ht[1] 哈希表只会在对 ht[0] 哈希表进行 rehash 时使用。

除了 ht[1] 之外，另一个和 rehash 有关的属性就是 rehashidx ：它记录了 rehash 目前的进度，如果目前没有在进行 rehash ，那么它的值为 -1 。

下图展示了一个普通状态下（没有rehash）的字典

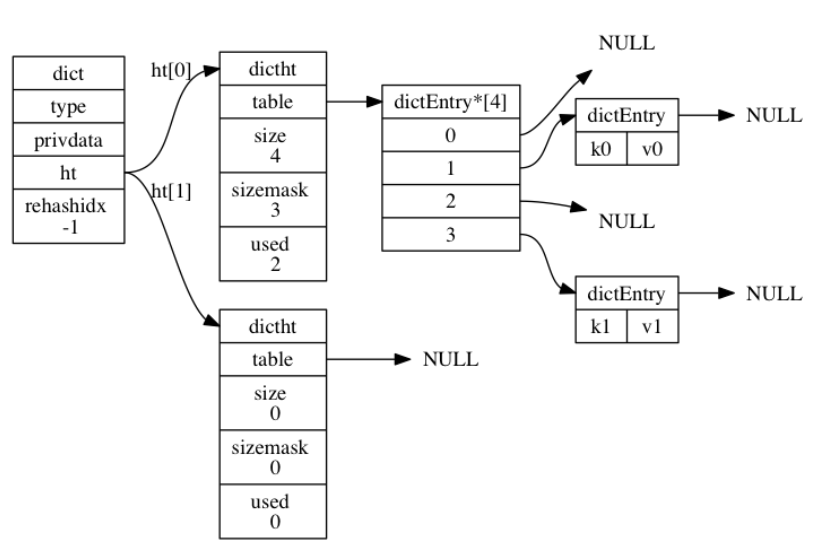
3.2 哈希算法

程序需要先根据键值对的键计算出哈希值和索引值，然后再根据索引值，将包含新键值对的哈希表节点放到哈希表数组的指定索引上面。

Redis 计算哈希值和索引值的方法如下：

// 使用字典设置的哈希函数，计算键 key 的哈希值
hash = dict->type->hashFunction(key);

// 使用哈希表的 sizemask 属性和哈希值，计算出索引值
// 根据情况不同， ht[x] 可以是 ht[0] 或者 ht[1]
index = hash & dict->ht[x].sizemask;

举个例子，假如想要将键值对k0 和 v0 添加到下面的字典中。

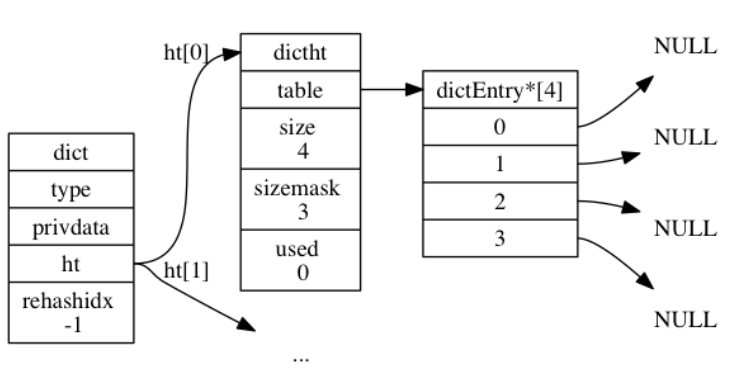
假设计算出的hash值是8，则index为

index = hash & dict->ht[0].sizemask = 8 & 3 = 0;

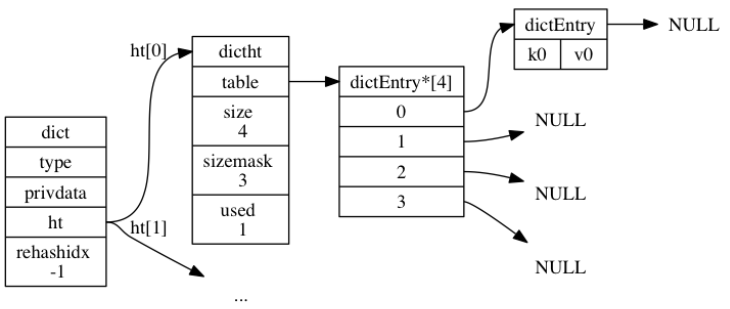
至于Redis的哈希值计算方法，使用的是 MurmurHash2。这种算法的优点在于，即使输入的键是有规律的，算法仍能给出一个很好的随机分布性，并且算法的计算速度也非常快。

3.3 Rehash

随着操作的不断执行，哈希表保存的键值对会逐渐地增多或者减少，为了让哈希表的负载因子（load factor）维持在一个合理的范围之内， 当哈希表保存的键值对数量太多或者太少时，程序需要对哈希表的大小进行相应的扩展或者收缩。

再哈希的关键在于重新分配哈希表的大小，分配的原则如下：

如果执行拓展操作ht[1] 的大小为第一个大于等于 ht[0].used * 2 的 $2^n$，比如原表大小为4，则 ht[0].used * 2结果为8，而8刚好是$2^3$，所以新的大小是8。
如果执行的是收缩操作，那么 ht[1] 的大小为第一个大于等于 ht[0].used 的$2^ n$

完成分配后，将保存在 ht[0] 中的所有键值对 rehash 到 ht[1] 上面，然后将 ht[1] 设置为 ht[0] ，并在 ht[1] 新创建一个空白哈希表，为下一次 rehash 做准备。

决定是否再Hash的要素来自于负载因子，计算方法如下：

//负载因子 = 哈希表已保存节点数量 / 哈希表大小
load_factor = ht[0].used / ht[0].size

3.4 渐进式Rehash

如果键值对很多，则将ht[0]重新hash到ht[1]上，则会导致服务器在一段时间内停止服务。为了避免这种问题，需要分多次渐进式的慢慢映射。

关键点在于维持一个索引计数器变量 rehashidx ，并将它的值设置为 0 ，表示 rehash 工作正式开始。

在 rehash 进行期间，每次对字典执行增删改查，程序除了执行指定的操作以外， 还会顺带将 ht[0] 哈希表在 rehashidx 索引上的所有键值对 rehash 到 ht[1] ，当 rehash 工作完成之后，程序将 rehashidx 属性的值增一。

完成后程序将 rehashidx 属性的值设为 -1 ，表示 rehash 操作已完成。

渐进式 rehash 的好处在于它采取分而治之的方式，将 rehash 键值对所需的计算工作均滩到对字典的每个增删改查上，从而避免了集中式 rehash 而带来的庞大计算量。

4. 跳跃表

4.1 什么是跳跃表

我们知道链表随机读写的能力很差，当增删改查的时候，如果要找到目标元素就需要遍历链表。假设某个数据结构是有序的，我们就会想到用二分法来快速查找，但链表是没有索引的，所以我们需要添加。

可以继续向上拓展层数：

但是我们的链表不是静态的，增加和删除会破坏二分结构，所以我们就不强制要求 1:2 了，一个节点要不要被索引，建几层的索引，都在节点插入时由随机决定。

现在假设节点 17 是最后插入的，在插入之前，我们需要搜索得到插入的位置：

4.2 跳跃表的实现

Redis 的跳跃表由 redis.h/zskiplistNode 和 redis.h/zskiplist 两个结构定义，其中 zskiplistNode 结构用于表示跳跃表节点，而 zskiplist结构则用于保存跳跃表节点的相关信息，比如节点的数量，以及指向表头节点和表尾节点的指针，等等。

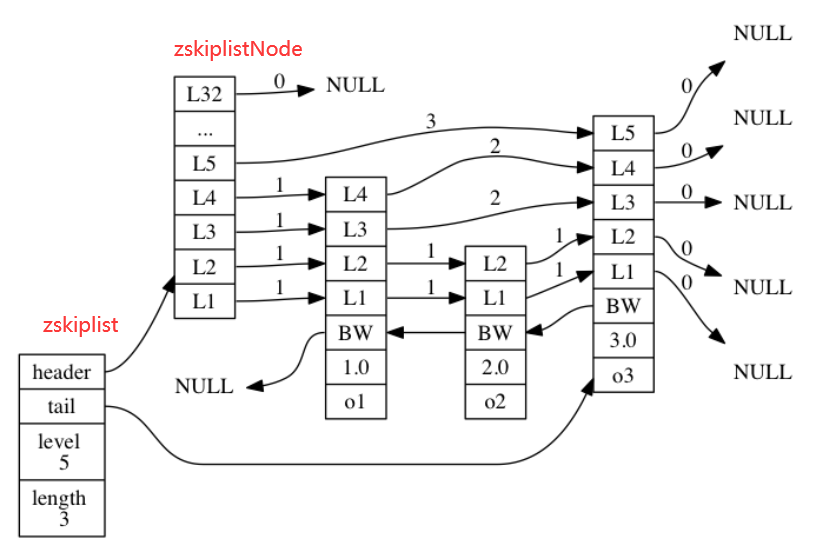
在zskiplist中level 记录目前跳跃表内最大层数（表头不算），length记录包含的节点数量（表头不算）。

zskiplistNode 结构包含以下属性：

层：每一层有两个属性
- 前进指针用于访问位于表尾方向的其他节点
- 跨度则记录了前进指针所指向节点和当前节点的距离。
后退指针(bw)：指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。
分值(score)：各个节点中的 1.0 、 2.0 和 3.0 是节点所保存的分值。用于从小到大排列。如果分值相同，则成员对象小的排在前面。
成员对象（obj）：各个节点中的 o1 、 o2 和 o3 是节点所保存的成员对象。

typedef struct zskiplistNode {
    // 后退指针
    struct zskiplistNode *backward;
    // 分值
    double score;
    // 成员对象
    robj *obj;
    // 层
    struct zskiplistLevel {
        // 前进指针
        struct zskiplistNode *forward;
        // 跨度
        unsigned int span;
    } level[];
} zskiplistNode;

（1）层

每次创建一个新跳跃表节点的时候，程序都根据幂次定律（power law，越大的数出现的概率越小）随机生成一个介于 1 和 32 之间的值作为 level 数组的大小，这个大小就是层的“高度”。

下图展示了三个高度为 1 层、 3 层和 5 层的节点

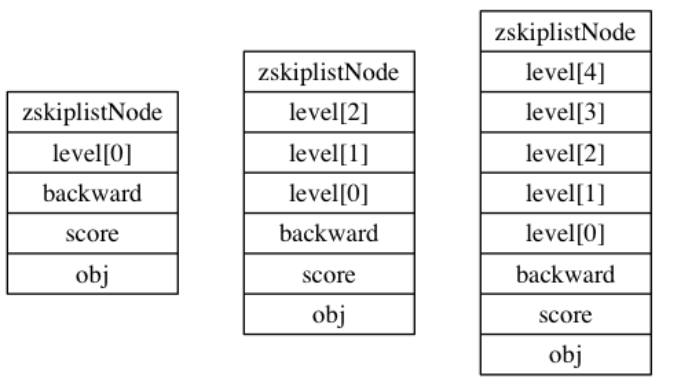
（2）前进指针

前进指针分属于不同的层，level[i].forward，用于从表头向表尾方向访问节点。

（3）跨度

跨度也分属不同的层，指向 NULL 的所有前进指针的跨度都为 0，因为它们没有连向任何节点。

跨度实际上是用来计算位次（rank）的： 将沿途访问过的所有层的跨度累计起来，得到的结果就是目标节点在跳跃表中的排位。

下图的例子中，查找分值为3.0的节点，由于只经过了一个层，跨度为3，所以跳跃表中的排位为3。

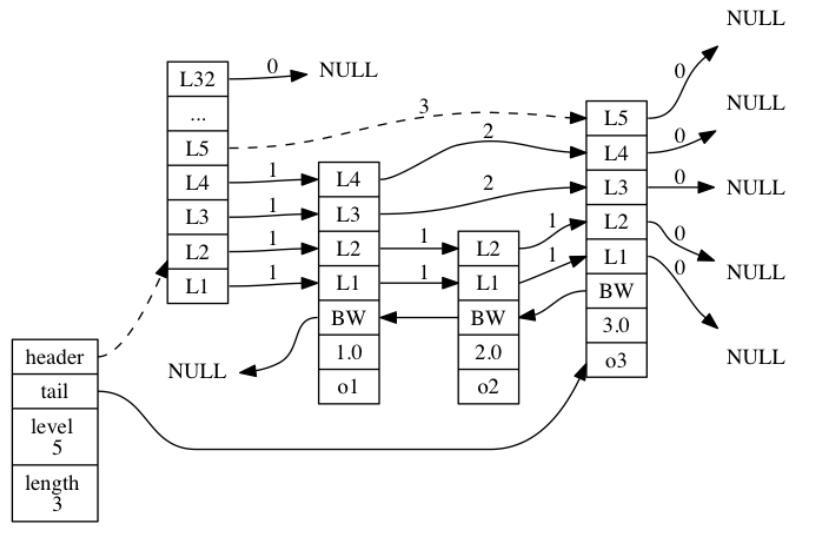
使用一个 zskiplist 结构来持有这些节点，程序可以更方便地对整个跳跃表进行处理。

typedef struct zskiplist {
    // 表头节点和表尾节点
    struct zskiplistNode *header, *tail;
    // 表中节点的数量
    unsigned long length;
    // 表中层数最大的节点的层数
    int level;
} zskiplist;

5. 整数集合

当一个集合中只包含整数，并且元素的个数不是很多的话，redis 会用整数集合作为底层存储，它可以节省很多内存。

5.1 整数集合的实现

整数集合（intset）是 Redis 用于保存整数值的集合抽象数据结构，它可以保存类型为 int16_t 、 int32_t 或者 int64_t 的整数值，并且保证集合中不会出现重复元素。

每个 intset.h/intset 结构表示一个整数集合：

typedef struct intset {
    // 编码方式
    uint32_t encoding;
    // 集合包含的元素数量
    uint32_t length;
    // 保存元素的数组
    int8_t contents[];
} intset;

contents 数组是整数集合的底层实现：整数集合的每个元素都是 contents 数组的一个数组项（item），从小到大有序地排列，不包含任何重复项。

虽然 intset 结构将 contents 属性声明为 int8_t 类型的数组，但实际上 contents 数组并不保存任何 int8_t 类型的值 —— contents 数组的真正类型取决于 encoding 属性的值：

encoding 为 INTSET_ENC_INT16，int16_t 类型的数组，范围$[-2^{16},2^{16}-1]$
encoding INTSET_ENC_INT32 ，是一个 int32_t 类型的数组。
encoding 为 INTSET_ENC_INT64 ，是一个 int64_t 类型的数组

下图展示了一个示例：

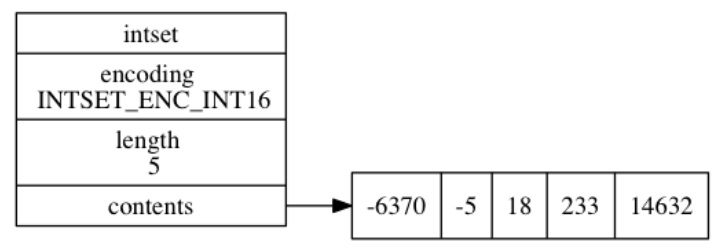
5.2 升级

每当我们要将一个新元素添加到整数集合里面，并且新元素的类型比整数集合元素的类型长时，整数集合需要先进行升级（upgrade），然后才能将新元素添加到整数集合里面。

过程如下：

根据新类型，扩展整数集合底层数组的空间大小，并为新元素分配空间
将底层数组现有的所有元素都转换成与新元素相同的类型，并将类型转换后的元素有序放置。
将新元素添加到底层数组里面。

假设想要在16位编码的intset中插入32位的65535数据，原来的集合是这样的：

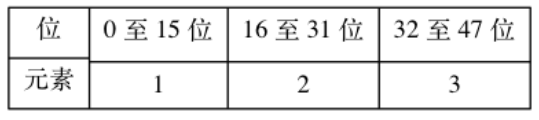
需要扩容为$32\times4=128$位，新intset结构会扩容成这样：

剩下就需要对元素重排。

先将3移动到新intset结构的索引2的位置上，然后将2移动到索引1的位置，然后将1移动到索引0的位置。最后再讲65535移动到索引3的位置。

5.3 降级

整数集合不支持降级操作，一旦对数组进行了升级，编码就会一直保持升级后的状态。

即使我们将集合里唯一一个真正需要使用 int64_t 类型来保存的元素 4294967295 删除了，整数集合的编码仍然会维持 INTSET_ENC_INT64。

6. 压缩列表

压缩列表（ziplist）是列表键和哈希键的底层实现之一。当一个列表键只包含少量列表项，并且每个列表项要么就是小整数值或长度比较短的字符串，那么 Redis 就会使用压缩列表来做列表键的底层实现。

6.1 压缩列表的构成

压缩列表是 Redis 为了节约内存而开发的，由一系列特殊编码的连续内存块组成的顺序型（sequential）数据结构。

属性	类型	长度	作用
zlbytes	uint32_t	4字节	整个压缩列表占用内存字节数
zltail	uint32_t	4字节	记录表尾节点距离表起始地址有多少个字节
zllen	uint16_t	2字节	记录节点数量
entryX		不定	节点
zlend	uint8_t	1字节	用于标记末端

下面展示了一个例子：

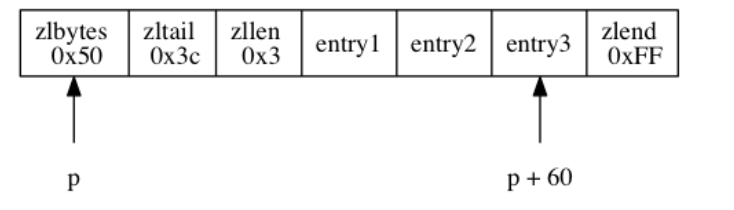
zlbytes 属性的值为 0x50 （十进制 80），表示压缩列表的总长为 80 字节。
zltail 属性的值为 0x3c （十进制 60），如果一个指向压缩列表起始地址的指针 p ，那么只要用指针 p 加上偏移量 60 ，就可以计算出表尾节点 entry3 的地址。
zllen 属性的值为 0x3 （十进制 3），表示压缩列表包含三个节点。

6.2 压缩列表的节点构成

每个压缩列表节点可以保存一个字节数组或者一个整数值，其中，字节数组可以是以下三种长度的其中一种：

长度小于等于63($2^6-1$)字节的字节数组；
长度小于等于 16383 ($2^{14}-1$)字节的字节数组；
长度小于等于 4294967295 ($2^{32}-1$)字节的字节数组；

而整数值则可以是以下六种长度的其中一种：

4 位长，介于 0 至 12 之间的无符号整数；
1 字节长的有符号整数；
3 字节长的有符号整数；
int16_t 类型整数；
int32_t 类型整数；
int64_t 类型整数。

每个压缩列表节点都由 previous_entry_length 、 encoding 、 content 三个部分组成。

（1）previous_entry_length

以字节为单位，记录了压缩列表中前一个节点的长度。这个属性的长度可以是1字节或5字节，如果前一个小于254则使用1字节，反之使用5字节（其中属性的第一字节会被设置为 0xFE（十进制值 254），而之后的四个字节则用于保存前一节点的长度）

程序可以通过指针运算，根据当前节点的起始地址来计算出前一个节点的起始地址。进而可以回溯到表头。

（2）encoding

节点的 encoding 属性记录了节点的 content 属性所保存数据的类型以及长度。编码由8位组成。

如果是字符类型，则开头两位00,01,10分别表示1字节，2字节，5字节，后6位表示字符串长度。

保存每个元素是1个字节的数组，长度11。

如果是整数类型，则开头必是11，然后从第6位开始往低位开始计数：

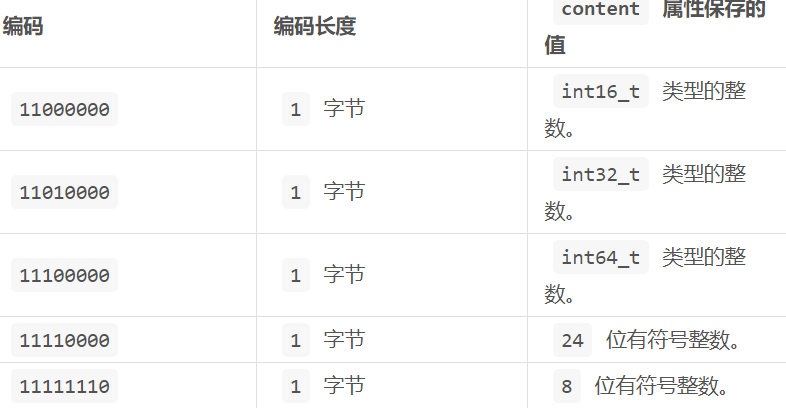
每个元素int16_t，值为10086

6.3 连锁更新

每个节点的 previous_entry_length 属性都记录了前一个节点的长度：

如果前一节点的长度小于 254 字节，那么 previous_entry_length 属性需要用 1 字节长的空间来保存这个长度值。
如果前一节点的长度大于等于 254 字节，那么 previous_entry_length 属性需要用 5 字节长的空间来保存这个长度值。

假设现在有一些长度为252字节的节点，他们在previous_entry_length中保存为1字节。现在插入了一个260字节的新节点，new 将成为 e1 的前置节点。

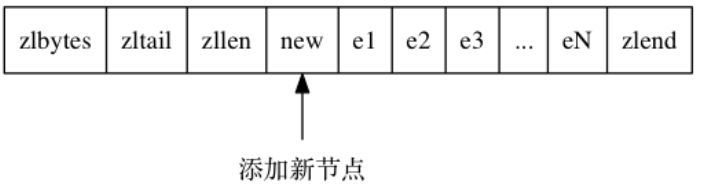
因为 e1 的 previous_entry_length 属性仅长 1 字节，它没办法保存新节点 new 的长度，所以程序将对压缩列表执行空间重分配操作， 并将e1 节点的 previous_entry_length 属性从原来的 1 字节长扩展为 5 字节长。

由于previous_entry_length 的变化，导致e1的长度也发生了变化$252+4=256>254$，所以导致e2也必须更新它的previous_entry_length 。这就是连锁更新。

除了添加节点外，删除节点也会导致连锁更新，若删除一个260字节的节点，则后一个节点长度也会变化。如果很不凑巧，小于254，则又会引起后序效应。

连锁更新在最坏情况下需要对压缩列表执行 N 次空间重分配操作，而每次空间重分配的最坏复杂度为$O(N)$ ，所以连锁更新的最坏复杂度为 $O(N^2)$ 。

Redis设计与实现1-数据结构

2020-01-02
数据库

Redis设计与实现1-数据结构

1. 简单动态字符串

1.1 SDS的定义

1.2 SDS 与 C 字符串的区别

2. 链表

3. 字典

3.1 字典的实现

3.2 哈希算法

3.3 Rehash

3.4 渐进式Rehash

4. 跳跃表

4.1 什么是跳跃表

4.2 跳跃表的实现

5. 整数集合

5.1 整数集合的实现

5.2 升级

5.3 降级

6. 压缩列表

6.1 压缩列表的构成

6.2 压缩列表的节点构成

6.3 连锁更新

Redis设计与实现1-数据结构

1. 简单动态字符串

1.1 SDS的定义

1.2 SDS 与 C 字符串的区别

2. 链表

3. 字典

3.1 字典的实现

3.2 哈希算法

3.3 Rehash

3.4 渐进式Rehash

4. 跳跃表

4.1 什么是跳跃表

4.2 跳跃表的实现

5. 整数集合

5.1 整数集合的实现

5.2 升级

5.3 降级

6. 压缩列表

6.1 压缩列表的构成

6.2 压缩列表的节点构成

6.3 连锁更新

感谢支持！