三维刚体运动主要分为旋转和平移,其中最重要最难的就是旋转。本文介绍了三种表示旋转的办法:旋转矩阵,旋转向量,四元数。
1. 旋转矩阵
1.1 向量积
质点在空间中可由 $xyz$ 坐标确定,但如果考虑刚体,需要考虑姿态问题。
点积$\mathbf {a \cdot b}=x_1x_2+y_1y_2+z_1z_2$,表示两个向量在同一方向的乘积。叉积表示垂直于两个方向的积。
点积可以描述向量间的投影关系。叉积可以表示向量的旋转。对于外积,我们引入了 $∧$符号,把 a 写成一个矩阵。事实上是一个反对称矩阵 (Skew-symmetric),可以将 $∧$ 记成一个反对称符号。这样就把外积 $a×b$,写成了矩阵与向量的乘法 $a∧b$,把它变成了线性运算。
我们可以用一个向量来描述三维空间中两个向量的旋转关系。在右手法则下,我们用右手的四个指头从 a 转向 b,其大拇指朝向就是旋转向量的方向,事实上也是 $a×b$ 的方向。a 到 b 的旋转可以由向量 $\mathbf{w}$ 来描述。
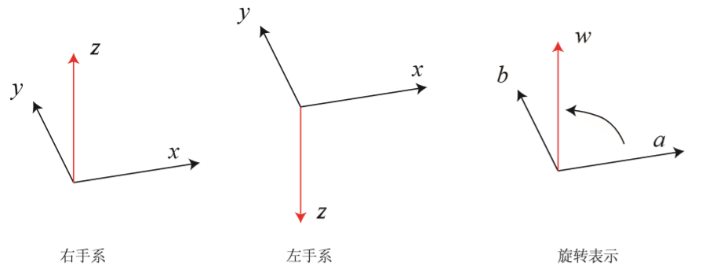
1.2 坐标系的欧氏变换
我们可以描述两个坐标系之间的旋转和平移,统称为坐标系之间的变换关系。欧氏变换则是指同一个向量在各个坐标系下的长度和夹角都不会发生变化。比如把手机抛到空中,在它落地摔碎之前,只可能有空间位置和姿态的不同,而它自己的长度、各个面的角度等性质不会有任何变化。
每一个欧氏变换由旋转和平移组成。
首先考虑旋转。我们设某个单位正交基 $(e_1,e_2,e_3)$ 经过一次旋转,变成了 $(e_1’ ,e_2’,e_3’)$ 。那么,对于同一个向量 $\mathbf{a}$(注意该向量并没有 随着坐标系的旋转而发生运动,它在两个坐标系下的坐标为 $[a_1,a_2,a_3]^T$ 和 $[a_1’,a_2’,a_3’]^T$。 根据坐标的定义
为了描述两个坐标之间的关系,我们对上面等式左右同时乘$\begin{bmatrix} e1^T \ e 2^T\ e_3^T \end{bmatrix}$
那么左边的系数变成了单位矩阵。
我们把中间的阵拿出来,定义成一个矩阵 $R$ ,这个矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的,那么 这个矩阵也是一样的, $R$ 就是旋转矩阵
旋转矩阵是一个行列式为 1 的正交矩阵(orthogonal matrix)。反之,行列式为1的正交矩阵也是一个旋转矩阵。
它的逆(即转置)描述了一个相反的旋转。即 $R^T$ 刻画了一个相反的旋转。
正交矩阵的转置和逆矩阵相等,正交矩阵与转置矩阵相乘得到单位矩阵
然后考虑平移。考虑世界坐标系中的向量 $\mathbf{a}$,经过一次旋转(用 $R$ 描述)和一次平移 $t$ 后,得到了 ,那么$\mathbf{a’}$把旋转和平移合到一起,有:
1.3 变换矩阵与齐次坐标
我们把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。对于这个四维向量,我们可以把旋转和平移写在一个矩阵里面,使得整个关系变成 了线性关系。矩阵 T 称为变换矩阵(Transform Matrix)。
2. 旋转向量与欧拉角
2.1 旋转向量
由旋转矩阵来描述旋转,变换矩阵描述一个六自由度的三维刚体运动,但这样过于冗余。旋转矩阵有九个量,但一次旋转只有三个自由度。变换矩阵用十六个量表达了六自由度的变换。需要使用新的表达方式来精简。
外积可以将两个向量的旋转关系表达为一个向量,即任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角(为了更紧凑的表达,旋转轴的长度为旋转角)。这种向量,称为旋转向量。这种表示法只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。
假设有一个旋转轴为 $\mathbf{n}$,角度为 $θ$ 的旋转,显然,它对应的旋转向量为 $θ\cdot \mathbf{n}$ 。旋转向量与旋转矩阵的转化方式可以由罗德里格斯公式表明:
2.2 欧拉角
无论是旋转矩阵、旋转向量,虽然它们能描述旋转,但对我们人类是非常不直观的。欧拉角使用三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。
- 绕物体的 Z 轴旋转,得到偏航角 yaw;
- 绕旋转之后的 Y 轴旋转,得到俯仰角 pitch;
- 绕旋转之后的 X 轴旋转,得到滚转角 roll。
这种旋转方式称之为rpy角。
欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock),若第二次旋转90°,则会使得物体与X轴垂直,使得系统丢失了一个自由度。
一般不会在程序中直接使用欧拉角表达姿态,同样不会在滤波或优化中使用欧拉角表达旋转。不过,若想验证自己算法是否有错时,转换成欧拉角能够快速辨认结果的正确与否。
3. 四元数
除了旋转向量和旋转矩阵表示旋转外,还可以采用四元数的形式。
3.1 四元数的定义
四元数拥有一个实部和三个虚部,可定义为:
其中$i,j,k$是四元数的三个虚部,满足关系式:
有时候也可以用一个标量和一个矢量来表示四元数:
$s$ 称为四元数的实部,而$v$ 称为它的虚部。如果一个四元数虚部为 0,称之为实四元数。反之,若它的实部为 0,称之为虚四元数。
假设某个旋转是绕单位向量$\textbf{n}=[n_x,n_y,n_z]^T$旋转了$θ$,那么这个旋转就可以用四元数表示为:
反之,我们亦可从单位四元数中计算出对应旋转轴与夹角:
3.2 四元数旋转
假设空间有三维点$p=[x,y,z]$,如果绕着轴$\mathbf{n}$以$θ$旋转,则将其表示为四元数形式有:
用四元数$q$表示这个旋转:
旋转后$p’$就可以表示为:
上面描述了某个点的旋转,下面表示的是如何由旋转四元数表示旋转矩阵:
反之旋转轴四元数也可以由旋转矩阵求取: