SLAM基础3-李群和李代数

李群和李代数是非常抽象的数学概念，在SLAM中我们通过他来衡量旋转平移的变化量。

1.基本概念

李群李代数主要用于SLAM算法中平移以及旋转来的求导。由于旋转矩阵为矩阵形式，不能用$R+\Delta R$表示变化量。

三维矩阵旋转构成了特殊正交群$SO(3)$，变换矩阵则构成了特殊欧式群$SE(3)$

$$\begin{array}{c}{S O(3)=\left\{\boldsymbol{R} \in \mathbb{R}^{3 \times 3} | \boldsymbol{R} \boldsymbol{R}^{T}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\}} \\ {S E(3)=\left\{\boldsymbol{T}=\left[\begin{array}{cc}{\boldsymbol{R}} & {t} \\ {0^{T}} & {1}\end{array}\right] \in \mathbb{R}^{4 \times 4} | \boldsymbol{R} \in S O(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\}}\end{array}$$

群（Group）是一种集合加上一种运算的代数结构。李群则是光滑的群(整数群就不光滑不连续)。李代数描述了李群的局部性质（变化率,相当于求导数）。

对于任意旋转矩阵$R$，由于它是正交矩阵，所以满足$RR^T=I$，如果$R$连续随时间变化，则我们用$R(t)$表示：

$$R(t)R(t)^T=I$$

对其求导可得：

$$\dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0\\ \dot{R}(t)R(t)^T=-R(t)\dot{R}(t)^T=-(\dot{R}(t)R(t)^T)^T$$

如果矩阵A满足$A^T=-A$，则称之为反对称矩阵。它的展开形式一定是:

$$\left[\begin{array}{ccc}{0} & {-a_{3}} & {a_{2}} \\ {a_{3}} & {0} & {-a_{1}} \\ {-a_{2}} & {a_{1}} & {0}\end{array}\right]$$

所以我们可以用向量$[a_1,a_2,a_3]\land$表示

由于$\dot{R}(t)R(t)^T$是一个反对称矩阵，我们可以找到一个三维向量 与之对应。于是有：

$$\dot{R}(t)R(t)^T=\phi(t)\land$$

等式左右两边乘以$R(t)$，由于$R$是正交矩阵，所以有：

$$\dot{\boldsymbol{R}}(t)=\phi(t)^{\wedge} \boldsymbol{R}(t)=\left[\begin{array}{ccc}{0} & {-\phi_{3}} & {\phi_{2}} \\ {\phi_{3}} & {0} & {-\phi_{1}} \\ {-\phi_{2}} & {\phi_{1}} & {0}\end{array}\right] \boldsymbol{R}(t)$$

可以看到，每对旋转矩阵求一次导数，只需左乘一个 $\phi(t)\land$ 矩阵即可。为方便讨论，我们设 $t_0=0$，并设此时旋转矩阵为 $R(0)=I$，按照导数定义，可以把 $R(t)$ 在 0 附近进行 一阶泰勒展开：

$$\begin{aligned} \boldsymbol{R}(t) & \approx \boldsymbol{R}\left(t_{0}\right)+\dot{\boldsymbol{R}}\left(t_{0}\right)\left(t-t_{0}\right) \\ &=\boldsymbol{I}+\phi\left(t_{0}\right)^{\wedge}(t) \end{aligned}$$

同时在 $t_0$ 附近，设$\phi$ 保持为常数$\phi(t_0)=\phi_0$(保证$\phi{}$在 $t_0 $附近保持不变)则可以推导得出：

$$\dot{\boldsymbol{R}}(t)=\phi\left(t_{0}\right)^{\wedge} \boldsymbol{R}(t)=\phi_{0}^{\wedge} \boldsymbol{R}(t)$$

解微分方程可以得到：

$$\boldsymbol{R(t)}=\exp({\phi_0}^{\land} t)$$

由此可知给定某时刻的 $R$，我们就能求得一个 $\phi$，它描述了 $R$ 在局部的导数关系，它是一个李代数。

2. 映射关系

以下关系专门针对三维矩阵旋转构成了特殊正交群$SO(3)$，变换矩阵构成的特殊欧式群$SE(3)$，$\mathfrak{so}(3)$表示特殊正交群的李代数，此时旋转通过对数映射用$\phi$表示，$\mathfrak{se}(3)$表示特殊欧式群的李代数，变换用$\xi$

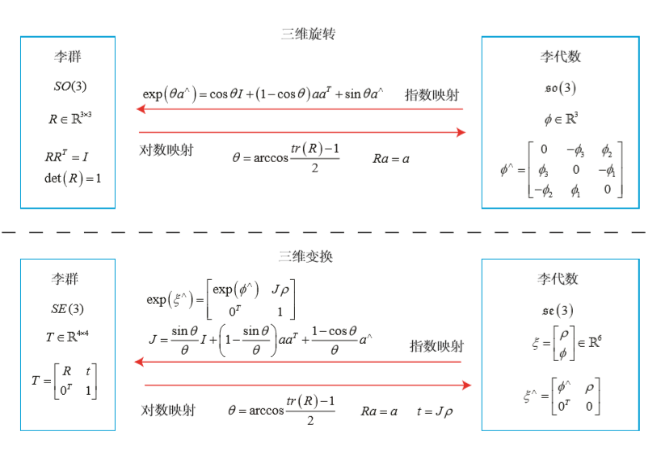
2.1 SO(3)上的映射

$\exp(ϕ∧)$ 是如何计算的？它是一个矩阵的指数，在李群和李代数中，称为指数映射（Exponential Map）

任意矩阵的指数映射可以写成一个泰勒展开：

$$exp(A)=\sum_{n=0}^\infty{\frac{1}{n!}A^n}$$

替换A得到：

$$exp(\phi\land)=\sum_{n=0}^\infty{\frac{1}{n!}(\phi\land)^n}$$

对于反对称矩阵有两条特殊性质：

$$a^\land a^\land=aa^T-I\\ a^\land a^\land a^\land=-a^\land$$

展开可以得到：

$$\begin{aligned} \exp \left(\phi^{\wedge}\right) &=\exp \left(\theta \boldsymbol{a}^{\wedge}\right)=\sum_{n=0} \frac{1}{n !}\left(\theta \boldsymbol{a}^{\wedge}\right)^{n} \\ &=\boldsymbol{I}+\theta \boldsymbol{a}^{\wedge}+\frac{1}{2 !} \theta^{2} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\frac{1}{3 !} \theta^{3} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\frac{1}{4 !} \theta^{4}\left(\boldsymbol{a}^{\wedge}\right)^{4}+\ldots \\ &=\boldsymbol{a} \boldsymbol{a}^{T}-\boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\theta \boldsymbol{a}^{\wedge}+\frac{1}{2 !} \theta^{2} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}-\frac{1}{3 !} \theta^{3} \boldsymbol{a}^{\wedge}-\frac{1}{4 !} \theta^{4}\left(\boldsymbol{a}^{\wedge}\right)^{2}+\ldots \\ &=\boldsymbol{a} \boldsymbol{a}^{T}+\left(\theta-\frac{1}{3 !} \theta^{3}+\frac{1}{5 !} \theta^{5}-\ldots\right) \boldsymbol{a}^{\wedge}-\left(1-\frac{1}{2 !} \theta^{2}+\frac{1}{4 !} \theta^{4}-\ldots\right) \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge} \\ &=(1-\cos \theta) \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\boldsymbol{I}+\sin \theta \boldsymbol{a}^{\wedge} \\ &=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{a} \boldsymbol{a}^{T}+\sin \theta \boldsymbol{a}^{\wedge} \end{aligned}$$

最后就得到了类似罗德里格斯公式的式子：

$$\exp(\theta a^\land)=\cos(\theta)I+(1-\cos\theta)aa^T+\sin(\theta)a^\land$$

罗德里格斯公式如下：

$$\mathbf{R}=\cos\theta \mathbf\cdot \mathbf{I}+(1-\cos\theta)\mathbf{nn^T}+\sin\theta\cdot \mathbf{n} {\land}$$

因此我们可以知道，$\mathfrak{so}(3)$ 实际上就是由所谓的旋转向量组成的空间，而指数映射即罗德里格斯公式

反之也可以定义对数映射：

$$\phi=\ln (\boldsymbol{R})^{\vee}=\left(\sum_{n=0}^{\infty} \frac{(-1)^{n}}{n+1}(\boldsymbol{R}-\boldsymbol{I})^{n+1}\right)^{\vee}$$

2.2 SE(3)上的指数映射

相较于之前，我们把旋转矩阵$R$替换为变换矩阵$T$：

$$\begin{equation} \mathbf{\dot{T}}(t) = \mathbf{\xi}^\wedge(t) \mathbf{T}(t) \end{equation}$$

解微分方程可以得到：

$$\mathbf{T(t)}=\exp({\xi_0}^{\land} t)$$

仿照前面的指数展开可以得到：

$$\begin{aligned} \exp \left(\boldsymbol{\xi}^{\wedge}\right) &=\left[\begin{array}{cc}{\sum_{n=0}^{\infty} \frac{1}{n !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n}} & {\sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} \boldsymbol{\rho}} \\ {0^{T}} & {1}\end{array}\right] \\ & \triangleq\left[\begin{array}{cc}{\boldsymbol{R}} & {\boldsymbol{J} \boldsymbol{\rho}} \\ {\boldsymbol{0}^{T}} & {1}\end{array}\right]=\boldsymbol{T} \end{aligned}$$

右上角的 $J$ 可整理为：

$$J=\frac{\sin \theta}{\theta} I+\left(1-\frac{\sin \theta}{\theta}\right) a a^{T}+\frac{1-\cos \theta}{\theta} a^{\wedge}$$

3. 李代数求导

3.1 BCH公式与近似形式

在$SO3$中完成两个矩阵乘法时，在$\mathfrak{so}(3)$是否对应着加法？如果成立的话，相当于：

$$\exp(\phi_1^\land)\exp(\phi_2^\land)=\exp((\phi_1+\phi_2)^\land)$$

换言之，我们需要研究下述公式是否成立：

$$\ln(\exp(A)\exp(B))=A+B$$

然而这个式子在矩阵时并不成立，他真实的成立条件由BCH公式给出：

$$\ln \left( {\exp \left( A \right)\exp \left( B \right)} \right) = A + B + \frac{1}{2}\left[ {A,B} \right] + \frac{1}{12}\left[ {A,\left[ {A,B} \right]} \right] - \frac{1}{12}\left[ {B,\left[ {A,B} \right]} \right] + \cdots$$

其中[ ]为李括号。

一般来说李括号$\left[ {A,B} \right] = AB - BA$，若满足$\mathbf{\phi}$为反对称矩阵，则李括号的结果为：

$$[\phi_1,\phi_2]=(\Phi_1\Phi_2-\Phi_2\Phi_1)^\lor$$

取近似项可得：

$$\begin{equation} \ln {\left( {R_1}{R_2} \right)^ \vee } \approx \left\{ \begin{array}{l} {J_l}{\left( {\phi _2} \right)^{ - 1}}{\phi _1} + {\phi _2}\\ {J_r}{\left( {\phi _1} \right)^{ - 1}}{\phi _2} + {\phi _1} \end{array} \right. \end{equation}$$

在 $\phi_1$ 较小时，使用第一个式；在在 $\phi_2$ 较小时，使用第二个式（换句话说依据是左乘一个微小位移还是右乘）。

以第一个近似为例。该式告诉我们，当对一个旋转矩阵 $R_2$李代数为 $\phi_2$左乘一个微小旋转矩阵 $R_1$李代数为 $\phi_1$时，可以近似地看作，在原有的李代数 $\phi_2$ 上，加上了一 项 ${J_l}{\left( {\phi _2} \right)^{ - 1}}{\phi _1}$

这里的 $J_l$ 和 $J_r$ 也称为左/右雅可比——从而李代数就分成了左右两种模型（因此，李代数程序库会声明它使用的是左乘模型还是右乘模型）

这两个雅克比矩阵可以表示为如下形式，他和旋转向量$\theta a$的关系

$$\begin{equation} {J_l} = J = \sum\limits_{n = 0}^\infty {\frac{1}{\left( {n + 1} \right)!}{\left( {\phi ^ \wedge } \right)}^n} ,{J_r} = J\left( { - \phi } \right) \end{equation}$$

雅克比矩阵表示的是m个n元函数的一阶导数组成的矩阵

$$\mathbf{J}=\left[\begin{array}{ccc}{\frac{\partial \mathbf{f}}{\partial x_{1}}} & {\cdots} & {\frac{\partial \mathbf{f}}{\partial x_{n}}}\end{array}\right]=\left[\begin{array}{ccc}{\frac{\partial f_{1}}{\partial x_{1}}} & {\cdots} & {\frac{\partial f_{1}}{\partial x_{n}}} \\ {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial f_{m}}{\partial x_{1}}} & {\cdots} & {\frac{\partial f_{m}}{\partial x_{n}}}\end{array}\right]$$

3.2 李代数求导模型

假设我们对一个空间点 $p$ 进行了旋转，得到了 $R_p$。现 在，要计算旋转之后点的坐标相对于旋转的导数，我们记为：

$$\frac{\partial(Rp)}{\partial R}$$

按照李代数的写法：

$$\frac{\partial(\exp(\phi^\land)p)}{\partial\phi}$$

按照3.1所推导的结论：

$$\begin{aligned} \frac{\partial\left(\exp \left(\phi^{\wedge}\right) \boldsymbol{p}\right)}{\partial \boldsymbol{\phi}} &=\lim _{\delta \phi \rightarrow 0} \frac{\exp \left((\phi+\delta \phi)^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{\exp \left(\left(\boldsymbol{J}_{l} \delta \phi\right)^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi} \\ & \approx \lim _{\delta \phi \rightarrow 0} \frac{\left(\boldsymbol{I}+\left(\boldsymbol{J}_{l} \delta \phi\right)^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{\left(\boldsymbol{J}_{l} \delta \phi\right)^{\wedge} \exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\delta \phi}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{J}_{l} \\ &=\lim _{\delta \phi \rightarrow 0} \frac{-\left(\exp \left(\phi^{\wedge}\right) \boldsymbol{p}\right)^{\wedge} \boldsymbol{J}_{l} \delta \phi}{\delta \phi}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{J}_{l} \end{aligned}$$

第二行的近似为 BCH 线性近似，第三行为泰勒展开舍去高阶项后近似，第四行至第 五行将反对称符号看作叉积，交换之后变号。于是，我们推导了旋转后的点相对于李代数的导数：

$$\frac{d\left( {RP} \right)}{d\phi }= {(-RP)^ \wedge }{J_l}$$

得到的结果中包含雅克比矩阵，我们希望进一步简化，因此可以采用扰动模型。

3.3 扰动模型

上一种求导方式比较复杂，下面介绍另一种另一种求导方式，是对 $R$ 进行一次扰动 $∆R$。这个扰动可以乘在左边也可以乘在右 边，最后结果会有一点儿微小的差异。

假设我们对一个空间点 $p$ 进行了旋转，得到了 $R_p$。现 在，要计算旋转之后点的坐标相对于旋转的导数，我们记为：

$$\frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}}=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\varphi}$$

这里和李代数求导模型有很大区别，李代数求导模型是老老实实按照求导定义来的，因此出现了李代数加法从而引出了雅克比矩阵，而扰动模型用乘法来近似。

近似后可以得到：

$$\begin{aligned} \frac{\partial(\boldsymbol{R} p)}{\partial \varphi} &=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) p-\exp \left(\phi^{\wedge}\right) p}{\varphi} \\ & \approx \lim _{\varphi \rightarrow 0} \frac{\left(1+\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) p-\exp \left(\phi^{\wedge}\right) p}{\varphi} \\ &=\lim _{\varphi \rightarrow 0} \frac{\varphi^{\wedge} R p}{\varphi}=\lim _{\varphi \rightarrow 0} \frac{-(R p)^{\wedge} \varphi}{\varphi}=-(R p)^{\wedge} \end{aligned}$$

同理在SE3上的李代数求导结果为

$$\frac{\partial(\boldsymbol{T} \boldsymbol{p})}{\partial \delta \boldsymbol{\xi}}=\left[\begin{array}{cc}{\boldsymbol{I}} & {-(\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t})^{\wedge}} \\ {\boldsymbol{0}^{T}} & {\boldsymbol{0}^{T}}\end{array}\right] \triangleq(\boldsymbol{T} \boldsymbol{p})^{\odot}$$

其中⊙算符把一个4×4的矩阵变换成一个4×6的矩阵，计算方式如下：

$$\begin{equation} p = \left[ \begin{array}{l} x_{3 \times 1}\\ w_{1 \times 1} \end{array} \right], \quad {p^ \odot } = \left[ {\begin{array}{*{20}{c}} w{I_{3 \times 3}}&{ - {x^ \wedge }_{3 \times 3}}\\ {0^T}_{3 \times 1}&{0^T}_{3 \times 1} \end{array}} \right] \end{equation}$$