介绍高斯金字塔、拉普拉斯金字塔原理,以及他们的应用——图像融合。
1. 高斯金字塔
高斯金字塔本质上是信号的在不同尺度上的表达,即将同一图片多次进行高斯模糊,并向下采样,产生不同尺度下的多组信号或图片以进行后续的处理。
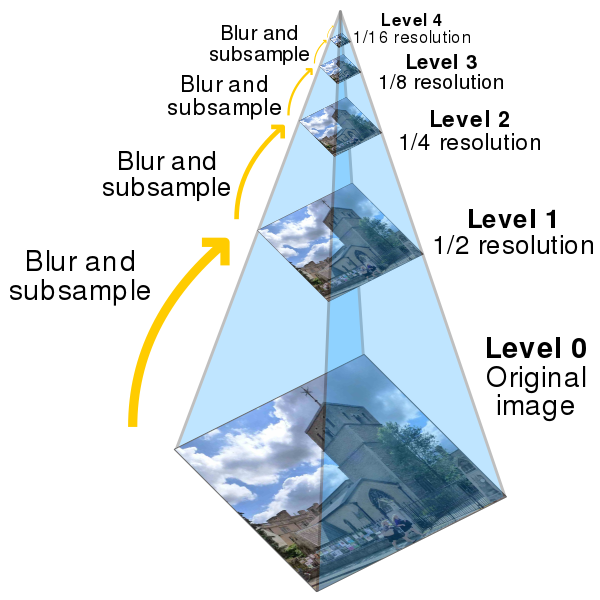
为了获取层级为$G_{i+1}$的金子塔图像,我们采用如下办法:
- 对图像$G_i$进行高斯平滑
- 将所有偶数行去除
得到的图像即为$G_{i+1}$的图像。显然,整个图像的大小只有原图的1/4。不断重复操作就能得到整个金字塔。
高斯内核如下:
降采样过程如下:
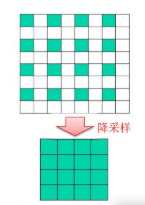
在Opencv中调用pyrDown函数即可,默认输出参数为Size((src.cols+1)/2, (src.rows+1)/2)
void cv::pyrDown ( InputArray src,
OutputArray dst,
const Size & dstsize = Size(),
int borderType = BORDER_DEFAULT
)

2. 拉普拉斯金字塔
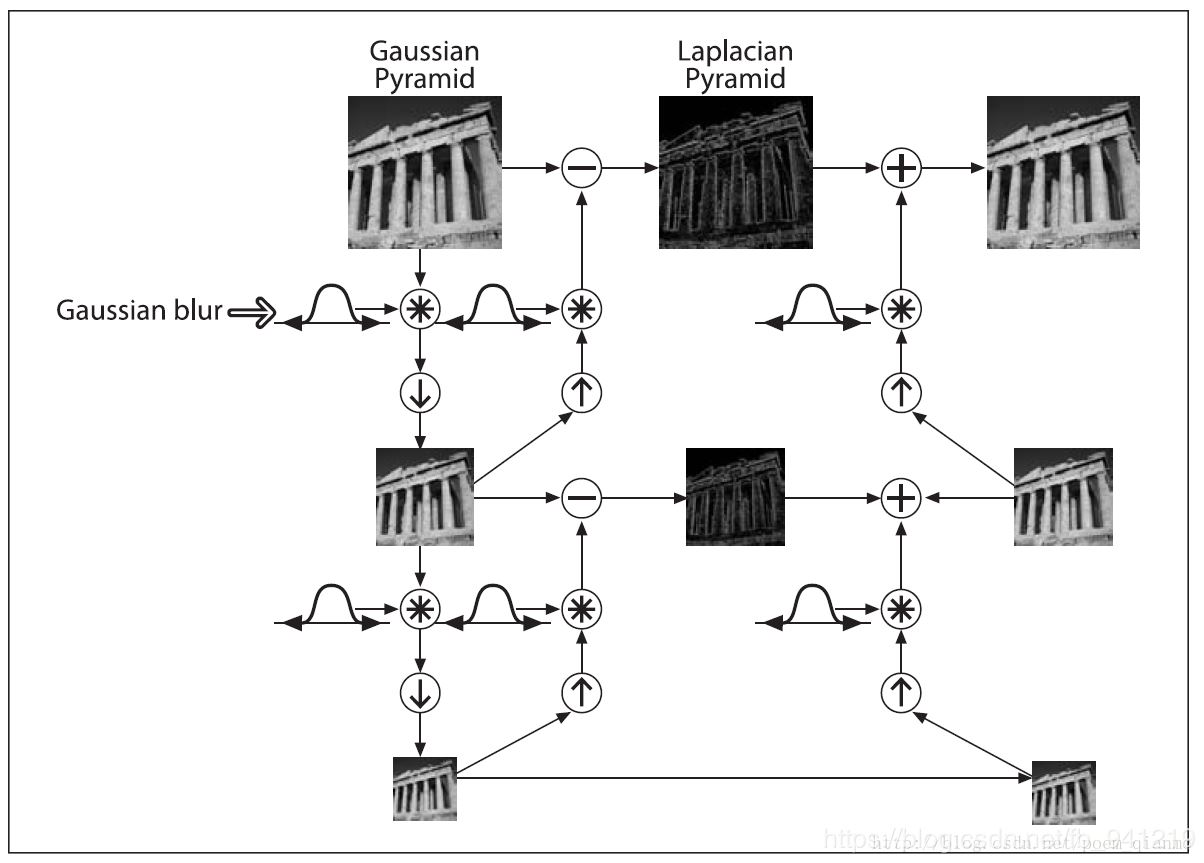
拉普拉斯金字塔式高斯金字塔的逆过程,又称差分金字塔(DOG)。
假设我们现在拥有高斯采样图$G_{i + 1}$和$G_i $,则拉普拉斯金字塔计算方式如下:
- 将$Gi $每列每行赋值一遍,插入到隔行隔列中间,这样图像$G{i+1}^{\prime}$大小和$G_{i+1}$相同
- 两者做差$G{i+1}^{\prime}-G{i+1}$,得到的结果就是拉普拉斯金字塔
同样的在opencv中也有:
void cv::pyrUp ( InputArray src,
OutputArray dst,
const Size & dstsize = Size(),
int borderType = BORDER_DEFAULT
)

3. 金字塔的应用-图像融合
如12所示,我们能够按如下方法得到图像的高斯金字塔和拉普拉斯金字塔:
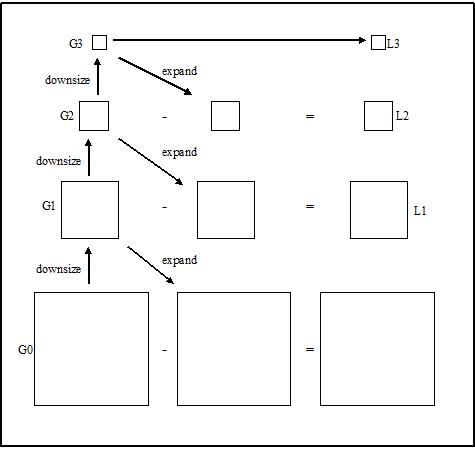
在最底层,我们认为高斯等于拉普拉斯,由此我们希望以此为开始,融合两张图片。
首先我们需要准备一个掩模M

通过掩模对两张图像的拉普拉斯每一层做运算,然后相加:
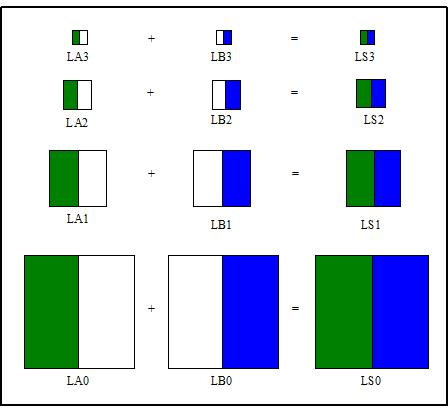
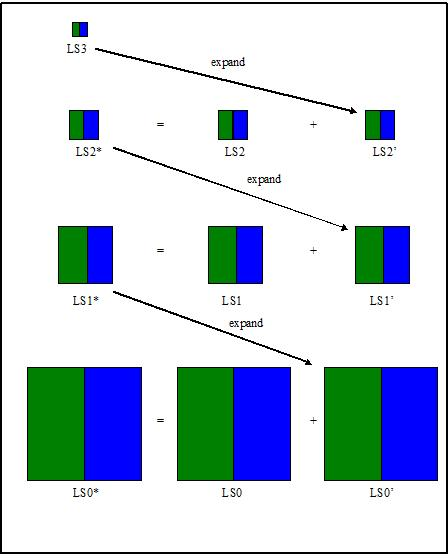
随后将得到的图片进行扩展,然后加上下一层的图片:
另一种简单的办法是feathr blending,对于交接区域我们做简答的加权即可。

这种办法对图像的质量要求很高,如果两张图片存在曝光差异(exposure differences),算法结果就会很差。
