SLAM基础6-后端

前一章讲的非线性优化方法其实是后端优化中的一个工具。后端需要对前端传来的传感信息进行优化，方法有卡尔曼滤波和光束法平差BA两种。

1. 经典的后端优化方法

1.1 状态估计的概率解释

视觉里程计只有短暂的记忆，在后端优化中，我们通常考虑一个更长时间内（或所有时间内）的状态估计问题，而且不仅使用过去的信息更新自己的状态，也会用未来的信息来更新自己。

$$\begin{equation} \left\{ \begin{array}\\ x_k=f(x_{k-1},u_k,\omega_k) \\ z_{k,j}=h(y_j,x_k,v_{k,j}) \end{array} \right. \end{equation}$$

运动方程和观测方程组成了SLAM系统，每个方程都受噪声影响，所以要把这里的位姿 $x$ 和路标 $y$ 看成服从某种概率分布的随机变量，而不是单独的一个数。因此整个问题变成了：当我拥有某些运动数据 $u$ 和观测数据 $z$ 时，如何来确定状态量 $x,y$ 的分布？

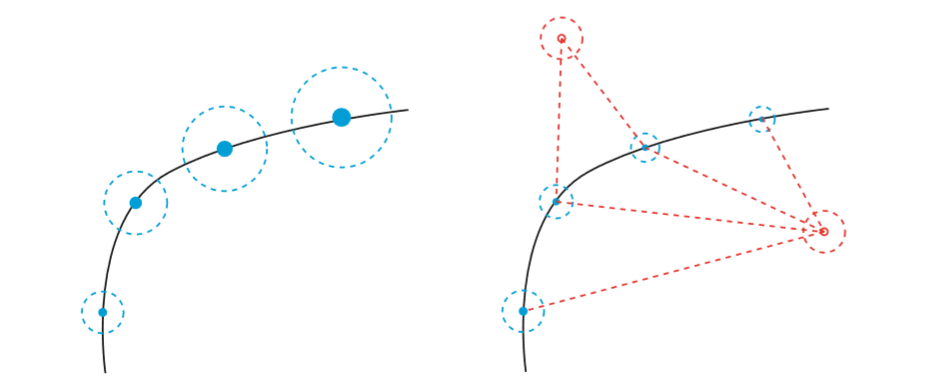
当没有观测数据，只有运动方程时，如左图所示，噪声导致的误差会逐渐累积，不确定性越来越大。如果我们可以观测路标点，误差会得到修正，不确定性就会减小。

下面以定量的角度思考。令$x_k$为$k$时刻的所有未知量，它包含了当前时刻的相机位姿和$m$个路标点。

$$x_k=(x_k,y_1,...,y_m)​$$

>同时，把$k$时刻的所有观测记为$z_k$，$u_k$还是表示传感器输入，整个方程可以写得比较简单。

$$\begin{equation} \left\{ \begin{array}\\ x_k=f(x_{k-1},u_k)+w_k\\ z_k=h(x_k)+v_k \end{array} \right. \end{equation}$$

现在考虑第$k$时刻的情况。我们希望用过去0到$k$的数据，来估计现在的状态分布：

$$P(x_{k}|x_{0},u_{1:k},z_{1:k})$$

下标 $0:k$表示从 0 时刻到 k 时刻的所有数据。请注意 $z_k$ 来表达所有在k时刻的观测数据，注意它可能不止一个，只是这种记法更加方便。这个式子表达了：已知初始位姿、之前所有的观测数据和传感器数据，通过这些条件来估计$k$时刻的位姿。

按照贝叶斯法则，展开可得：

$$P(x|x_{0},u_{1:k},z_{1:k})\propto P(z_{k}|x_{k})P(x_{k}|x_{0},u_{1:k},z_{1:k-1})$$

左边为后验概率，右边第一项为似然概率（已知数据求模型参数），第二项为先验概率。似然概率可以由观测方程计算得到，至于先验概率，我们知道当前状态$x(k)$是根据过去所有状态估计得到，所以他至少会受到$x(k-1)$的影响，于是在此处按照条件概率展开：

$$P(x_{k}|x_{0},u_{1:k},z_{1:k-1})=\int P(x_{k}|x_{k-1},x_{0},u_{1:k},z_{1:k-1})P(x_{k-1}|x_{0},u_{1:k},z_{1:k-1})d_{x_{k-1}}$$

如果我们考虑更久之前的状态，也可以继续对此式进行展开，但现在我们只关心 $k$ 时刻和 $k−1$ 时刻的情况。

后续的处理有两种方式：其一是假设马尔可夫性，即k 时刻状态只与k−1时刻状态有关，而与再之前的无关；其二依然考虑 k 时刻状态与之前所有状态的关系。前一种得到的方法是扩展卡尔曼滤波(EKF)，第二种得到非线性优化。

1.2 线性系统和KF

按照马尔科夫性，状态只与上一个时刻有关，因此公式可以进行简化。

$$P(x_{k}|x_{0},u_{1:k},z_{1:k})=\int P(x_{k}|x_{k-1},x_{0},u_{1:k},z_{1:k-1})P(x_{k-1}|x_{0},u_{1:k},z_{1:k-1})d_{x_{k-1}}$$

由于$k$时刻的状态与$k-1$之前无关，所以可以简化为只与$x_{k-1}$和$u_k$相关的形式，所以第一项可以简化为：

$$P(x_{k}|x_{k-1},x_{0},u_{1:k},z_{1:k-1})=P(x_{k}|x_{k-1},u_{k})$$

第二项由于输入量$u_k$与$k-1$无关，所以可以将其去掉：

$$P(x_{k-1}|x_{0},u_{1:k},z_{1:k-1})=P(x_{k-1}|x_{0},u_{1:k-1},z_{1:k-1})$$

可以看到这就是$k-1$时刻的状态分布（参照贝叶斯法则展开前$P(x{k}|x{0},u{1:k},z{1:k})$）。我们实际在做的是“如何把 k−1 时刻的状态分布推导至 k 时刻”这样一件事。

首先从简单的线性高斯系统开始。

$$\left\{ \begin{matrix} x_{k}=A_{k}x_{k-1}+u_{k}+w_{k} \\ z_{k}=C_{k}x_{k}+v_{k}\ \end{matrix}\right.$$

第一个公式描述状态量$xk$，$A_k$是状态转移矩阵，负责描述$x{k-1}$时刻到$x_k$的状态，$u_k$是控制矩阵，是k-1到k状态改变的原因，$w_k$是噪声。

第二个公式描述观测量$z_k$，$C_k$时观测矩阵，$v_k$是噪声。并假设所有的状态和噪声均满足高斯分布。记这里的噪声服从零均值高斯分布：

$$w_k\sim N(0,R),\ v_k\sim N(0,Q)$$

假设我们已知$x{k-1}$状态分布的后验状态估计$\overset{\wedge }{x}{k-1}$和协方差$\overset {\wedge }x{k-1}$根据输入数据和观测数据，确定$x_k$的后验分布。$\overset{\wedge }x{k}$表示后验，$\overset{- }x_{k}$表示先验。

高斯分布运算性质：

$$x+y\sim N(\mu_x+\mu_y,\sum _{xx}+\sum_{yy})$$

若$y=\textbf{A}x$，则y满足：

$$y\sim N(A\mu,A\sum_{xx}A^T)$$

所以有：

$$P(x_{k}|x_{0},u_{1:k},z_{1:k-1})=N(A_{k}\overset{-}{x}_{k-1}+u_{k},A_{k}\overset{-}{P}_{k-1}A_{k}^{T}+R)=N(\overset{-}{x}_{k},\overset{-}{P}_{k})$$

因此我们得到了两个公式：状态预测公式，协方差预测公式

$$\overset{-}{x}_{k}=A_{k}\overset{-}{x}_{k-1}+u_{k}\\ \overset{-}{P}_{k}=A_{k}\overset{-}{P}_{k-1}A_{k}^{T}+R$$

这里$\overset{-}{x}{k}$表示先验分布，也就是不准确的，$\overset{\wedge }{x}{k}$表示的是后验分布，是经过修正的。

得到的这两个结果都是预测结果，他们需要通过观测方程来进行修正。由于计算过程太复杂，直接给出结果：

$$\overset{\wedge }{x}_{k}=\overset{- }{x}_{k}+K(z_{k}-C_{k}\overset{- }{x}_{k})\\ \overset{\wedge }{P}_{k}=(I-KC_{k})\overset{-}{P }_{ k}\\$$

计算出$\overset{\wedge }{P}_{k}$是为了留给下一次迭代使用。

这里的$K$表示卡尔曼系数，它具有两个作用：

• 决定相信预测模型$\overset{- }{x}_{k}$更多一些还是观测模型更多一些
• 将残差$(z{k}-C{k}\overset{- }{x}_{k})$的表现形式由观测域转化到状态域

卡尔曼系数的计算公式是：

$$K=\overset{\wedge }{P}_{k}C_{k}^{T}Q^{-1}=\overset{-}{P}_{k}{C}_{k}^{T}({C}_{k}\overset{-}{P}_{k}{C}_{k}^{T}+Q_{k})^{-1}$$

所以卡尔曼滤波可以由五个公式概括：

$$\begin{equation} \left\{ \begin{array}{lr} \overset{-}{x}_{k}=A_{k}\overset{-}{x}_{k-1}+u_{k}\\ \overset{-}{P}_{k}=A_{k}\overset{-}{P}_{k-1}A_{k}^{T}+R\\ \overset{\wedge }{x}_{k}=\overset{- }{x}_{k}+K(z_{k}-C_{k}\overset{- }{x}_{k})\\ \overset{\wedge }{P}_{k}=(I-KC_{k})\overset{-}{P }_{ k}\\ K=\overset{\wedge }{P}_{k}C_{k}^{T}Q^{-1}=\overset{-}{P}_{k}{C}_{k}^{T}({C}_{k}\overset{-}{P}_{k}{C}_{k}^{T}+Q_{k})^{-1} \end{array} \right. \end{equation}$$

前两个是预测公式，后两个是更新公式（将预测的先验值修正）。

1.3 非线性系统和EKF

卡尔曼滤波是针对线性方程，当系统非线性时需要通过一些操作来近似，这就是扩展卡尔曼滤波(Extended Kalman Filter, EKF)

EKF的做法主要有两点：

其一是在工作点$\overset{\wedge }{x}{k-1},\overset{-}{x}{k}$附近进行泰勒展开，将系统线性化：

$$\begin{array}{l}{f\left(x_{k-1}, v_{k}, w_{k}\right) \approx f\left(\hat{x}_{k-1}, v_{k}, 0\right)+\frac{\partial f}{\partial x_{k-1}}\left(x_{k-1}-\hat{x}_{k-1}\right)+\frac{\partial f}{\partial w_{k}} w_{k}} \\ {g\left(x_{k}, n_{k}\right) \approx g\left(\tilde{x}_{k}, 0\right)+\frac{\partial g}{\partial x_{k}} n_{k}}\end{array}$$

这里的偏导数都在工作点附近取值，最后变成了一个线性系统。

其二是在线性系统近似下，把噪声项和状态都当成了高斯分布。经过这两项近似以后得到的结果和普通卡尔曼滤波就一样了：

$$\begin{aligned} \tilde{P}_{k} &=F_{k-1} \hat{P}_{k-1} F_{k-1}^{T}+Q_{k}^{\prime} \\ \tilde{x}_{k} &=f\left(\hat{x}_{k-1}, v_{k}, 0\right) \\ K_{k} &=\tilde{P}_{k} G_{k}^{T}\left(G_{k} \tilde{P}_{k} G_{k}^{T}+R_{k}^{\prime}\right)^{-1} \\ \hat{P}_{k} &=\left(I-K_{k} G_{k}\right) \tilde{P}_{k} \\ \hat{x}_{k} &=\tilde{x}_{k}+K_{k}\left(y_{k}-g\left(\tilde{x}_{k}, 0\right)\right) \\ \mathbf{其中，}\\F_{k-1} &=\left.\frac{\partial f}{\partial x_{k-1}}\right|_{\hat{x}_{k-1}}, G_{k}=\left.\frac{\partial f}{\partial x_{k}}\right|_{\bar{x}_{k}} \end{aligned}$$

1.4 EKF的问题讨论

EKF主要有三个问题：

• 滤波器方法假设了马尔可夫性，也就是 k 时刻的状态只与 k−1 时刻相关，而与 k −1 之前的状态和观测都无关。这比较像视觉里程计的原理，但是如果当前帧确实和以前的数据有关（例如回环检测），滤波器就无法应对。

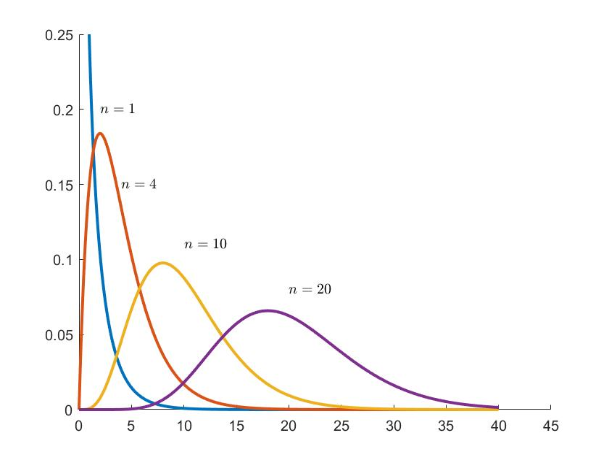
• 由非线性转化到线性时我们安排了两个假设：展开点取一次项，把噪声项和状态都当成了高斯分布。系统本身线性化过程中，丢掉了高阶项。即使是高斯分布，经过一个非线性变换后也不是高斯分布。举个例子，假设一个$x\sim N(0,1)$，那么$y=x^2$服从的是卡方分布，当卡方分布n较大时，比较接近高斯分布，这样我们就可以很好近似。但是当n比较小近似的结果就很差。

  

• 从程序实现上来说，EKF 需要存储状态量的均值和方差，并对它们进行维护和更新。 如果把路标也放进状态的话，由于视觉 SLAM 中路标数量很大，这个存储量是相当可观的，且与状态量呈平方增长（因为要存储协方差矩阵）。因此，EKF普遍被认为不可适用于大型场景SLAM。

2. 现代优化方法：BA与图优化

见专题