自适应直方图均衡化

介绍直方图均衡化，以及他的升级版。

1. 普通的直方图均衡化

直方图均衡化可以将灰度分布均匀化，调整对比度。

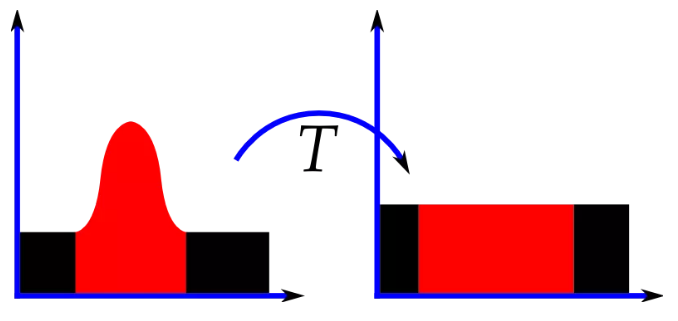
自适应的直方图均衡(Adaptive histogram equalization, AHE)是一种用于提升图像对比度的计算机图像处理技术。和普通的直方图均衡算法不同的点在于: 它计算那些指定区域的直方图，并用这些值去重新分配图像亮度来改变图像的对比度。

这种方法更适合改进图像的局部对比度和增强图像边缘来获得更多细节。

直方图均衡化利用累计分布函数(Cumulative distribution function, CDF)进行均衡，参照wiki的例子：

假设一个8×8的图像：

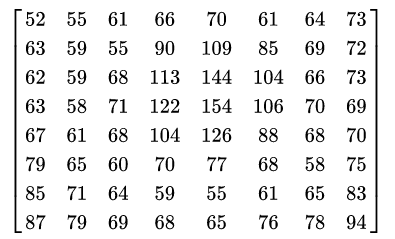
该灰度图像的灰度值出现次数如下表所示，为了简化表格，出现次数为0的值已经被省略。

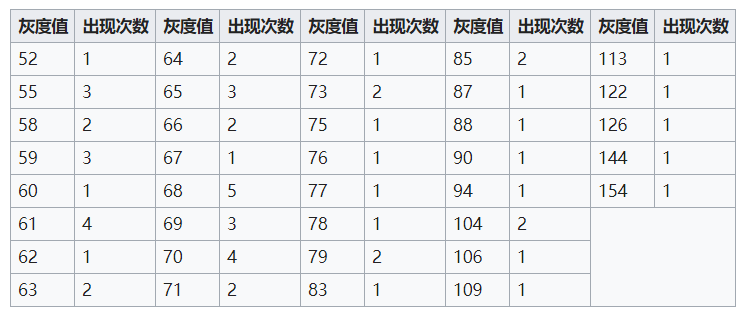
累积分布函数计算可以得到：

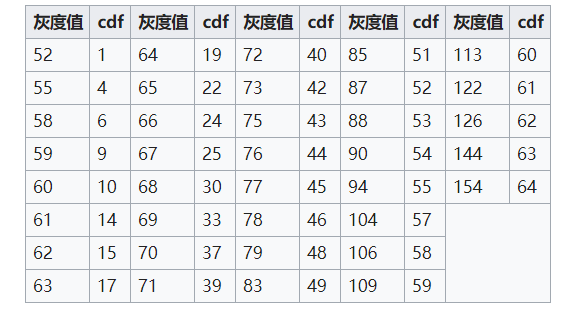
其中，灰度78的像素的累积分布函数为46，均衡化后灰度变化为：

$$h(78)=round(\frac{46-1}{64-1}\times255)=round(0.714\times255)=182$$

但是如果直方图存在明显的高峰，均衡化的结果就很不好。

下图就是一个例子。这幅图画面比较统一，因此高峰非常明显（太高了被PhotoShop截取了部分）

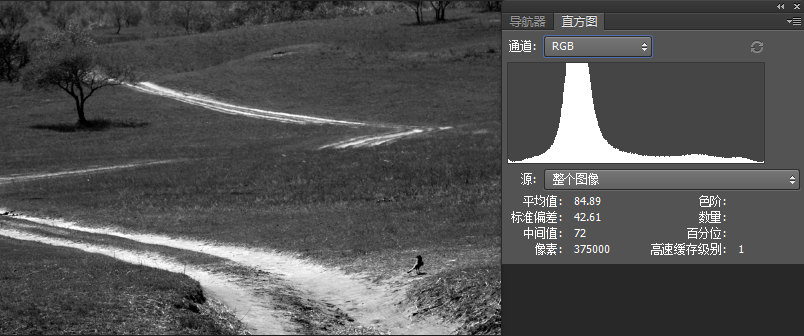
均衡化后：

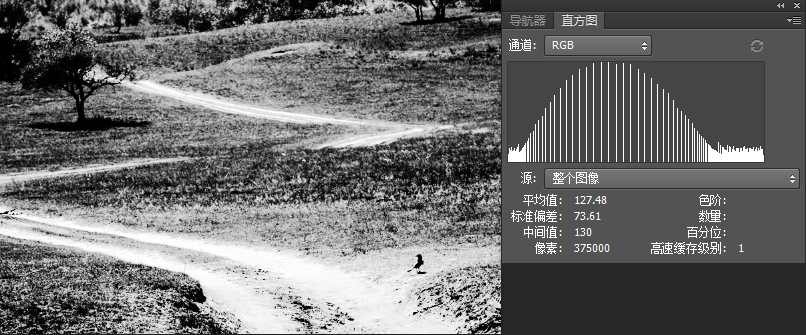
可以看到图像明显走样，对比度显得很不自然。

为了改善这样的情况，我们可以将计算的范围从整体缩小为局部 ，即每个像素通过其周围的一个矩形范围的像素直方图进行均衡化。这就是AHE的原理。

2. 限制对比度的自适应直方图均衡化

与AHE不同的是，CLAHE(Contrast Limited Adaptive Histogram Equalization )对每个小区域内的对比度都有限制。这主要是通过限制AHE的对比度提高程度来达到的。

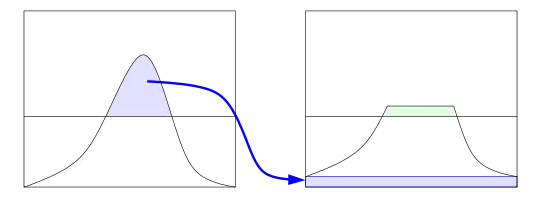
将局部直方图中超过阈值的部分截取，然后将它均匀分布到其他部分，可以保证整个直方图总面积不变。

为了提升计算速度及去除分块处理导致的块边缘过渡不平衡等问题，可以使用插值方法。如下图所示，AHE后图像呈块状：

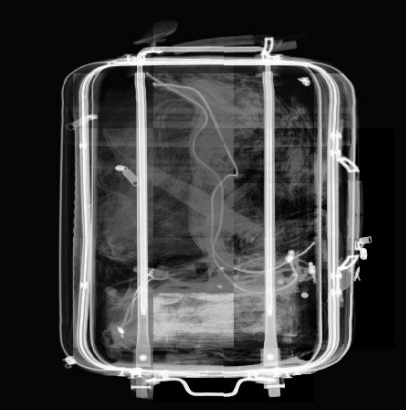
插值的方式是双线性插值，每个像素点出的值由它周围4个子块的映射函数值进行双线性插值得到，如下图：

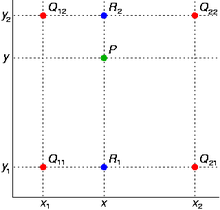
首先在 $x$ 方向进行线性插值：

$$\begin{aligned} f\left(x, y_{1}\right) & \approx \frac{x_{2}-x}{x_{2}-x_{1}} f\left(Q_{11}\right)+\frac{x-x_{1}}{x_{2}-x_{1}} f\left(Q_{21}\right) \\ f\left(x, y_{2}\right) & \approx \frac{x_{2}-x}{x_{2}-x_{1}} f\left(Q_{12}\right)+\frac{x-x_{1}}{x_{2}-x_{1}} f\left(Q_{22}\right) \end{aligned}$$

然后在 $y$ 方向插值：

$$f(x, y) \approx \frac{y_{2}-y}{y_{2}-y_{1}} f\left(x, y_{1}\right)+\frac{y-y_{1}}{y_{2}-y_{1}} f\left(x, y_{2}\right)$$

现在我可以通过四个点的像素值来预测一个点的像素值，也就是很常见的四点插值法 。这样做的好处就是不需要计算连续的像素值。相当于多重网格中，将细网格下降到粗网格，然后减少计算量。