ORB特征检测

ORB特征检测是由FAST角点检测和BRIEF描述子检测组合的检测手段，在ORBSLAM中有良好运用。

1. 基本概念

特征点指图像中选取比较有代表性的点，这些点在相机视角发生少量变化后会保持不变，所以我们会在各个图像中找到相同的点。

特征点由关键点（Key-point）和描述子（Descriptor）两部分组成。关键点是指该特征点在图像里的位置，有些特征点还具有朝向、大小等信息。描述子通常是一个 向量，描述了该关键点周围像素的信息。描述子是按照“外观相似的特征应该有相似的描述子”的原则设计的。

ORB （Oriented FAST and Rotated BRIEF）改进了 FAST 检测子不具有方向性的问题，并采用速度极快的二进制描述子 BRIEF，使整个图像特征提取的环节大大加速。借助尺度空间理论构建图像高斯金字塔，然后在每一层金字塔图像上检测角点，以实现尺度不变性。

ORB 特征亦由关键点和描述子两部分组成。它的关键点称为”Oriented FAST”，是 一种改进的 FAST 角点，它的描述子称为 BRIEF （Binary Robust Independent Elementary Features）。因此，提取 ORB 特征分为两个步骤：

1. FAST 角点提取：找出图像中的”角点”。相较于原版的 FAST, ORB 中计算了特征点的主方向，为后续的 BRIEF 描述子增加了旋转不变特性。
2. BRIEF 描述子：对前一步提取出特征点的周围图像区域进行描述。

2. Fast关键点

FAST 是一种角点，主要检测局部像素灰度变化明显的地方，以速度快著称。它的思想是：如果一个像素与它邻域的像素差别较大（过亮或过暗）, 那它更可能是角点。算法步骤如下：

1. 在图像中选取像素 $p$，假设它的亮度为 $I_p$。
2. 设置一个阈值 $T$(比如 Ip 的 20%)
3. 以像素 $p$ 为中心, 选取半径为 3 的圆上的 16 个像素点。
4. 假如选取的圆上，有连续的 $N$ 个点的亮度大于 $(I_p + T)$ 或小于 $(I_p −T)$，那么像素 p 可以被认为是特征点 ($N$ 通常取 12，即为 FAST-12。其它常用的 $N$ 取值为9和11， 他们分别被称为 FAST-9，FAST-11)。

在 FAST-12 算法中，为了更高效，可以添加一项预测试操作，以快速地排除绝大多数不是角点的像素。直接检测邻域圆上的第 1，5，9，13 个像素的亮度。只有当这四个像素中有三个同时亮度大于 $(I_p + T)$ 或小于 $(I_p −T)$，当前像素才有 可能是一个角点，否则应该直接排除。

FAST算子本身是不具有方向性的，因此我们需要引入距分析来完成oriented：

图像的距为：

$$m_{p q}=\sum_{x, y \in B} x^{p} y^{q} I(x, y), \quad p, q=\{0,1\}$$

质心为：

$$C=\left(\frac{m_{10}}{m_{00}}, \frac{m_{01}}{m_{00}}\right)$$

连接图像的几何中心O和质心C可以得到方向向量$\vec{OC}$，方向就可以被定义为：

$$\theta=\arctan{(m_{01}/m_{10})}$$

3. BRIEF描述子

BRIEF 是一种二进制描述子，它的描述向量由许多个 0 和 1 组成，这里的 0 和 1 编码了关键点附近两个像素（比如说 p 和 q）的大小关系：如果 p 比 q 大，则取 1，反之就取 0。如果我们取了 128 个这样的 pq，最后就得到 128 维由 0，1 组成的向量。

pq的选点在BRIEF中采取了随机选点的比较，速度很快。

算法步骤如下：

1. 以特征点P为中心，取一个S×S大小的Patch邻域；
2. 在这个邻域内随机取N对点(x,y)，比较N对像素点的灰度值的大小,如果x的灰度大于y，则写为1，反之为0
3. 重复步骤2得到N个（一般为256）二进制代码串

随机点的选择一般采用高斯分布的形式，匹配时采用汉明距离(两代码串同位不同的个数,比如010和101汉明距离为3)

原始的 BRIEF 描述子不具有旋转不变性，因此在图像发生旋转时容易丢失。原因是其采用了方形领域，当旋转时会造成覆盖的区域发生变化：

而 ORB 在 FAST 特征点提取阶段计算了关键点的方向，所以可以利用方向信息，计算了旋转之后的”Steer BRIEF”特征，使 ORB 的描述子具有较好的旋转不变性。

4. 尺度不变性

前面介绍了利用距分析获取特征方向从而实现旋转不变性，同样的我们也需要实现尺度不变性，我们在描述一个特征之前，将两张图像都变换同一个尺度上，然后再在这个统一标准上来描述这个特征。

为了实现尺度不变性，需要给特征加上尺度因子。在进行特征描述的时候，将尺度统一即可。一般采用高斯金字塔模型。

与普通的金子塔不同，我们进行分组构建：

1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层，将第1组第1层图像经高斯滤波之后作为第1组金字塔的第2层。
2. 将第一次滤波的方差$\sigma$乘以比例系数得到$\sigma_2=k\sigma_1$,用它来平滑第1组第2层图像，结果图像作为第3层。
3. 如此这般重复，最后得到L层图像，在同一组中，每一层图像的尺寸都是一样的，只是平滑系数不一样。它们对应的平滑系数分别为：$0，σ，kσ，k^2σ,k^3σ……k^(L-2)σ$
4. 将第1组倒数第三层图像作比例因子为2的降采样(缩小一倍)，得到的图像作为第2组的第1层，重复步骤2

这样反复执行，就可以得到一共O组，每组L层，共计O*L个图像，这些图像一起就构成了高斯金字塔，结构如下：

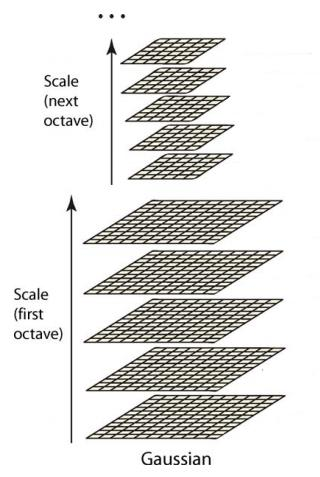
在高斯金字塔中一共生成O组L层不同尺度的图像，这两个量合起来（O，L）就构成了高斯金字塔的尺度空间，也就是说以高斯金字塔的组O作为二维坐标系的一个坐标，不同层L作为另一个坐标，则给定的一组坐标（O,L）就可以唯一确定高斯金字塔中的一幅图像。