鱼眼镜头模型

详细讲解鱼眼镜头的成像原理。

1. 鱼眼镜头原理

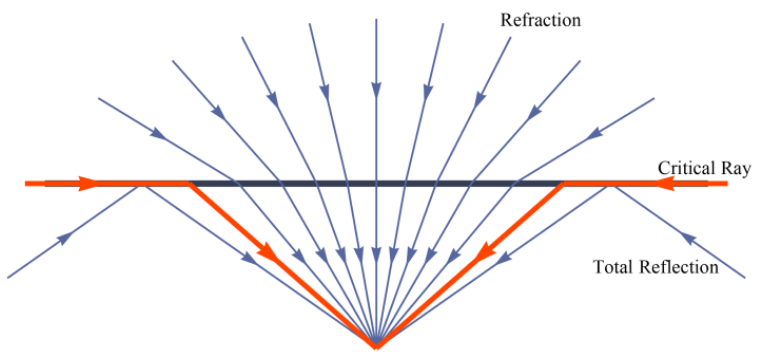
常见的相机模型是小孔模型，但小孔模型的视场比较小，即使采用超广角镜头视场也大概只有150°，很难做到全覆盖。因此人们利用鱼眼的特性发明了鱼眼镜头，能够达到接近180°的视场。

如图所示，小孔模型对于180°视场，只能将一部分投影到平面上，剩余的一小部分被截去了。

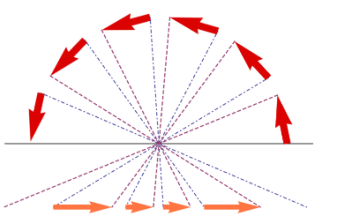
在自然界中，鱼眼能够通过水的折射，将光线压缩到一个锥形内

在这个锥形内部有一部分来自水面上方，有一部分来自水面下方，水面上方的所有景物都被压缩到了一个圈内，这就是斯涅耳窗口

如果这样拍一张照片，就可以在一个合理的照片大小范围内，记录整个水面上的半球空间内的景象。有效的视角范围接近 180°，远远超过普通超广角镜头记录的范围。鱼眼镜头与这个场景类似，也是把很大角度范围内的光线进行「压缩」和「扭曲」，压进一个相对较小的空间内，从而可以被相机所记录下来。

2. 鱼眼镜头模型

鱼眼镜头由一系列复杂的透镜组成，前两个透镜负责大力折射光线，后面的镜头负责成像。

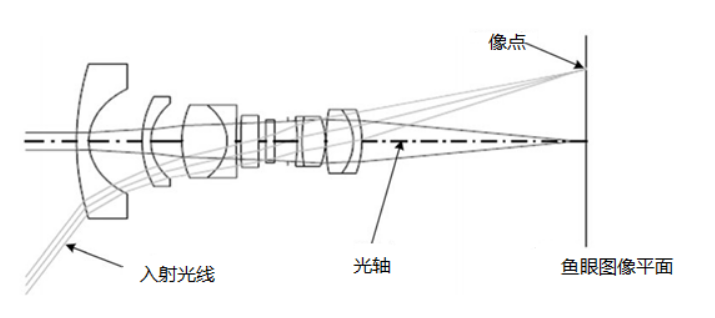
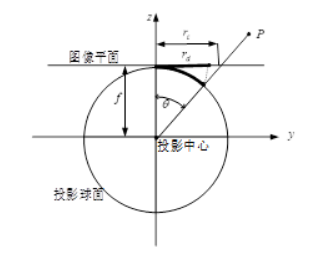
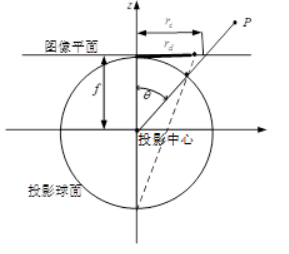
鱼眼相机成像时遵循的模型可以近似为单位球面投影模型。可以将鱼眼相机的成像过程分解成两步：

1. 三维空间点线性地投影到一个球面上，它是一个虚拟的单位球面，它的球心与相机坐标系的原点重合
2. 单位球面上的点投影到图像平面上，这个过程是非线性的

从球面投影到CCD平面的模型有很多种

• 等距投影 $r_d = f \theta$

• 等立体角投影 $r_d = 2fsin(\frac{\theta}{2})$

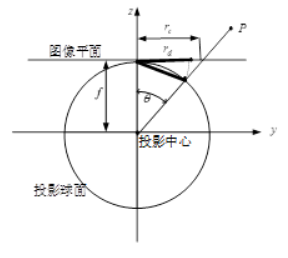
• 正交投影 $r_d = fsin( \theta)$

• 体视投影 $r_d = 2ftan(\frac{\theta}{2})$

3. Opencv中的鱼眼相机模型

由于投影方式多种多样，我们可以对其采用近似方法将其统一。观察可以发现，$\sin,\tan$的泰勒展开都是奇次项形式，取前5项可得即：

$$r_d =f\theta _d \\\theta_d= k_0\theta + k_1 \theta^3 + k_2 \theta^5 + k_3 \theta^7 + k_4 \theta^9$$

从空间点到鱼眼图像上的点的变换过程可用式子表示为：

$$\left[ \begin{array}{c} X_c \\ Y_c \\ Z_c \end{array} \right]=RX+t\\ x_c = \frac{X_c}{Z_c},\ y_c=\frac{Y_c}{Z_c}\\ r^2 = x^2_c + y^2_c\\ \theta = arctan(r)\\ \theta _d = k_0\theta + k_1 \theta^3 + k_2 \theta^5 + k_3 \theta^7 + k_4 \theta^9\\ x_d=\frac{\theta_d}{r}x_c, \ y_d=\frac{\theta_d}{r}y_c\\ u=f_xx_d+c_x, \ v=f_yy_d+c_y$$