光流法

光流法是计算机视觉中非常重要的方法，本文介绍了光流法的基本原理和提高精度的进阶办法。

1. 光流法基本原理

光流是一种描述像素随时间在图像之间运动的方法，随着时间的流逝，同一个像素会在图像中运动,我们可以追踪他的运动。

光流法应用的前提是灰度不变假设，也就是说$I(x_1,y_1,t_1)=I(x_2,y_2,t_2)$，虽然这是一个很苛刻的假设，但我们还是需要认为其在某些场景下具有合理性。

假设在$t+dt$的时刻某个像素运动到了$(x+dx,y+dy)$，我们可以得到：

$$I(x,y,t) = I(x+dx, y+dy,t+dt)$$

如果对上式中右侧进行一阶泰勒展开：

$$I(x+dx,y+dy,t+dt) \approx I(x,y,t)+\frac{\partial I}{\partial x}dx + \frac{\partial I}{\partial y}dy + \frac{\partial I}{\partial t}dt$$

根据灰度不变假设可以得到：

$$\frac{\partial I}{\partial x}dx + \frac{\partial I}{\partial y}dy + \frac{\partial I}{\partial t}dt = 0.$$

两侧同时除以$dt$，可以得到：

$$\frac{\partial I}{\partial x}\frac{dx}{dt} + \frac{\partial I}{\partial y}\frac{dy}{dt} = -\frac{\partial I}{\partial t}$$

其中 $\frac{dx}{dt},\frac{dy}{dt}$ 为像素在$x,y$轴上的运动速度，将他们记为 $u,v$。同时 $\frac{\partial I }{\partial x},\frac{\partial I}{\partial y}$ 记为图像在$x,y$方向上的梯度，分别记为$I_x,I_y$，把图像灰度对于时间的变化量记为 $I_t$，上面的式子可以表示为：

$$\begin{bmatrix} I_x&I_y \end{bmatrix} \begin{bmatrix} u\\ v \end{bmatrix} = - I_t$$

我们假设某个$W\times W$的窗口内的像素具有相同的运动，则：

$$A=\left[\begin{array}{c}{\left[I_{x}, I_{y}\right]_{1}} \\ {\vdots} \\ {\left[I_{x}, I_{y}\right]_{k}}\end{array}\right], b=\left[\begin{array}{c}{I_{t 1}} \\ {\vdots} \\ {I_{t k}}\end{array}\right]$$

简化后可得：

$$A\left[\begin{array}{l}{u} \\ {v}\end{array}\right]=-b$$

这是一个超定方程(方程个数大于未知数个数)，可以使用最小二乘法求解：

$$\begin{bmatrix} u\\ v \end{bmatrix}^* = -(A^TA)^{-1}A^Tb$$

超定方程组是指方程个数大于未知量个数的方程组，在方程$Ax=b$两边乘以$A^T$，所以该方程有唯一解且为原方程的最小二乘解：

$$\begin{equation} \begin{split} A^TAx=A^Tb \end{split} \\ x=(A^TA)^{-1}A^Tb \end{equation}$$

总结一下，光流法基于三个假设：

• 灰度不变，所以$I(x+dx,y+dy,t+dt) =I(x,y,t)$
• 小运动，所以我们可以取一阶泰勒展开
• 邻域内光流不变，所以我们可以取$W\times W$的小窗口

2. 金字塔光流法

光流法重要前提是小运动，也就是说图像随时间变化缓慢，这样灰度才能求偏导，最理想的条件当然是相邻帧图片间隔1个像素。为了解决运动过快导致的误差较大问题，我们可以通过减少图像中物体的位移。

缩小图像尺寸能有效减少位移，比如图像为400×400时，物体单位时间位移为[16,16]，那么当图像缩小为200×200时，位移变为[8,8]。缩小尺寸的办法可以使用金字塔分层。

高斯金字塔的概念在SIFT特征检测中已经详细说明。通过高斯金字塔能形成组（Octave）和层（Level或Interval）。

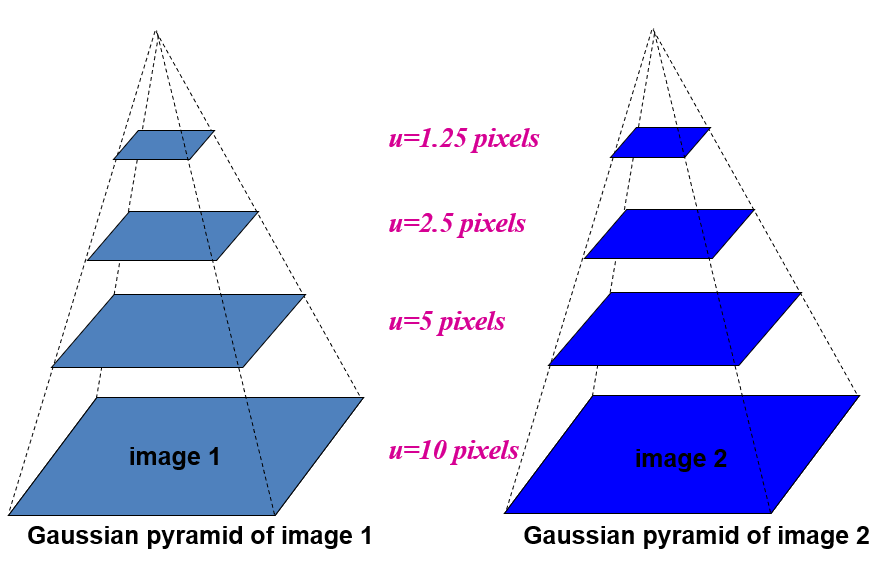
下面开始公式推导，假设$I,J$是两幅相邻运动图像。图像$I$的点$(x,y)$对应了图像$J$的点$(x+dx,y+dy)$，也就是说：

$$I(x,y)=J(x+dx,y+dy)$$

当然这之间肯定会存在误差，写出一片领域下的误差函数：

$$e=\sum_{x=u_{x}-\omega_{x}}^{u_{x}+\omega_{x}} \sum_{y=u_{y}-\omega_{y}}^{u_{y}+\omega_{y}}\left(I(x, y)-J\left(x+d_{x}, y+d_{y}\right)\right)^{2}$$

假设图像的尺寸每次缩放为原来的一半，共缩放了$Lm$组，第0组误差为$e(d)$，则每组的光流计算结果为为：

$$g(L)=\frac{g(0)}{2^L}$$

这并不是准确的结果，还得加上残差：

$$g(L)_{real}=g(L)+d(L)$$

反馈到第$L-1$层：

$$g(L-1)=2[g(L)+d(L)]$$

对于每一层，我们都希望光流的计算基于邻域内所有点匹配误差和最小化：

$$e(L)=\sum_{x=u_{x}^{L}-\omega_{x}}^{u_{x}^{L}+w_x} \sum_{y=u_{y}^{L}-\omega_{y}}^{u_{y}^{L}+\omega_{y}}\left(I^{L}(x, y)-J^{L}\left(x+g_{x}^{L}+d_{x}^{L}, y+g_{y}^{L}+d_{y}^{L}\right)\right)^{2}$$

具体算法是：

1. 利用最小二乘法计算最顶层的最小光流
2. 更新光流$v=2*v$，将光流方向传递到下一层，计算最小光流
3. 持续传递，直到传递到原图像输出