Harris特征检测

Harris是一种简单但实用的角点检测手段，本文介绍了他的基本原理，以及优劣势。

1. 基本原理

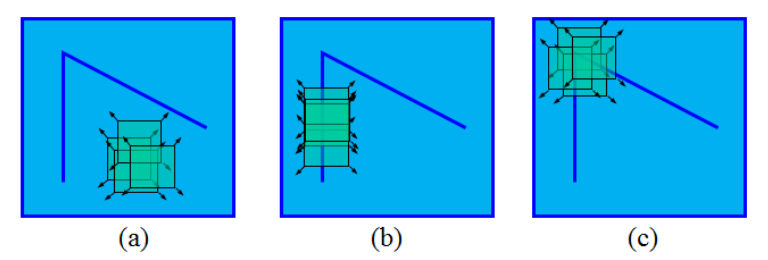
当一个窗口在图像上移动，在平滑区域如图(a)，窗口在各个方向上没有变化。在边缘上如图(b)，窗口在边缘的方向上没有变化。在角点处如图(c)，窗口在各个方向上具有变化。

假设图像窗口平移$[u,v]$产生的变化为$E(u,v)$则：

$$E(u, v)=\sum_{x_{s}, y} w(x, y)[I(x+u, y+v)-I(x, y)]^{2}$$

泰勒展开可得：

$$I(x+u, y+v)=I(x, y)+I_{x} u+I_{y} v+O\left(u^{2}, v^{2}\right)$$

这是单个像素的表达式，当发生微小位移时，忽略无穷小量。现在，我们考虑一个领域窗口内所有像素的移动情况，写成矩阵形式：

$$E(u, v)=\sum_w[u, v]\left[\begin{array}{cc}{I_{x}^{2}} & {I_{x} I_{y}} \\ {I_{x} I_{y}} & {I_{y}^{2}}\end{array}\right]\left[\begin{array}{l}{u} \\ {v}\end{array}\right]=[u, v]M\left[\begin{array}{l}{u} \\ {v}\end{array}\right]$$

假设梯度坐标表示为$(I_X,I_Y)$，，这个和上面有区别。不同的纹理特征表现出来的梯度坐标分布不同：

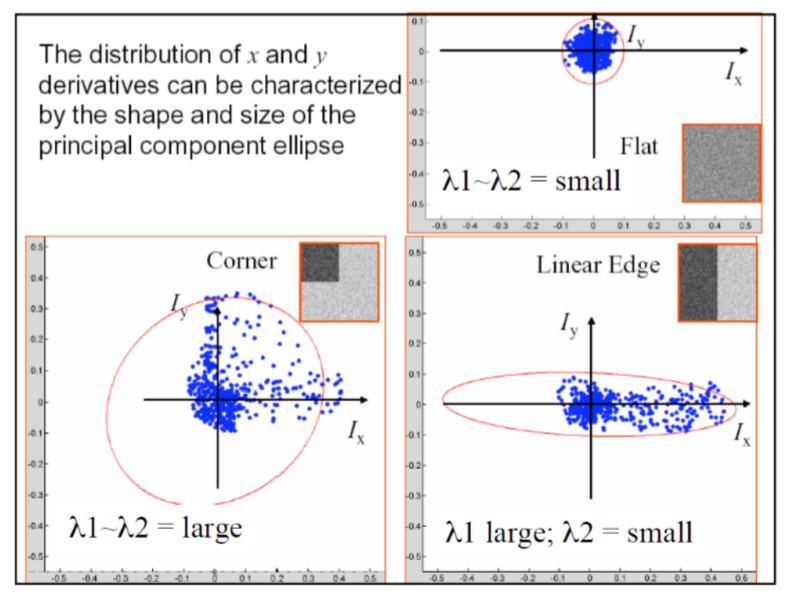
注意：样例图片并不是纯色，里面包含了很多的椒盐点，所以梯度分布才会出现散状。

可以看出，均匀图像的灰度在 $x,y$ 方向几乎没有变化，类似一个圆；边缘图像在某一个轴方向变化剧烈，在另一个方向没有变化，近似为一个扁椭圆；角点在两个方向变化都很剧烈，近似为一个卵型。

因此判断角点的条件就变为：长轴短轴都超过某一阈值，转化为矩阵语言就是$M$有两个大特征值。

2. 计算方法

由上可知，我们判断角点的依据就是特征值的大小

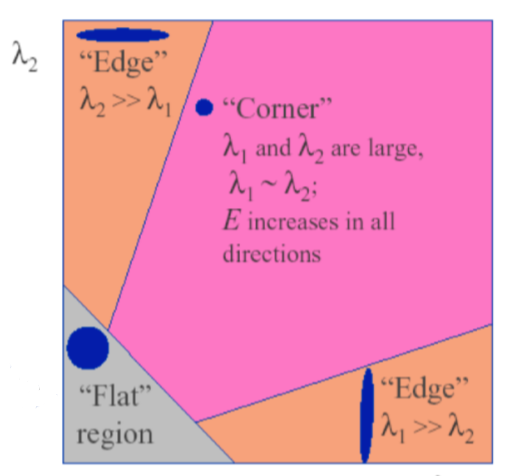
常规思路是进行SVD分解：

$$M=X\Sigma X^T = X \left[ \begin{matrix} \lambda_1& 0\\ 0& \lambda_2\end{matrix} \right] X^T$$

但速度比较慢，难以做到视频中实时监测的需求（30帧每秒），所以我们可以采用近似的做法：

$$M(x,y)=\Sigma_w \left[ \begin{matrix} I_x^2& I_xI_y \\ I_xI_y & I_y^2\end{matrix} \right] = \left[ \begin{matrix} A& C\\ C& B\end{matrix} \right]$$

采用近似的形式，$\alpha$一般取0.04-0.06：

$$R = detM-\alpha (traceM)^2\\ detM=\lambda_1 \lambda_2=AB-C^2\\ traceM=\lambda_1 + \lambda_2 = A+B$$

此时判断条件变为：

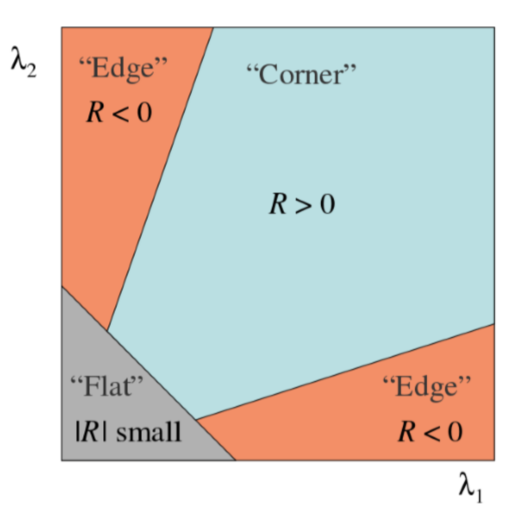
3. 性质

一般来说计算的角点会呈块状分布

所以我们需要使用非极大抑制(Non-maxima suppression)处理，得到单个的角点：

---

Harris角点对亮度和对比度的变化并不敏感

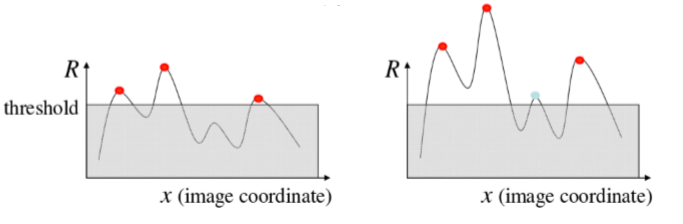
对于亮度来说，整体的上升和下降，并不影响角点的检测。对于对比度来说，按比例拉伸曲线，并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

---

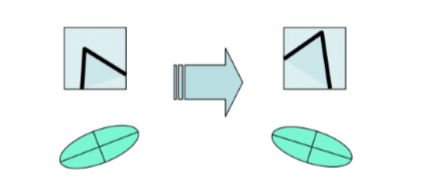
Harris角点检测算子具有旋转不变性。Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

---

Harris角点不具有尺度不变性。当图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

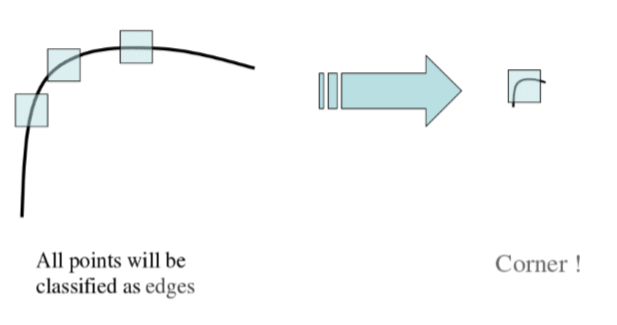
随着尺度的减小，能检测到角点数量也相应降低。