超定方程就是方程个数大于未知数的方程组,本文介绍了如何用最小二乘法解这样的方程。
1. 奇异值分解原理
1.1 特征值的数学含义
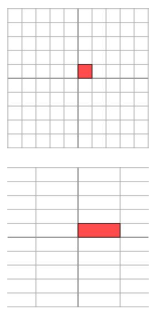
对角矩阵$M$作用在任何一个向量上:
换言之这个变换让$x$方向拉伸了3倍,$y$方向保持不变,对角矩阵起到作用是将水平垂直网格作水平拉伸(或者反射后水平拉伸)的线性变换。
对于一个一般矩阵$M=\begin{bmatrix}1&1\0&1 \end{bmatrix}$,我们可以找到一组网格,然后通过旋转+拉伸的方法保证变换后的网格依旧互相垂直。
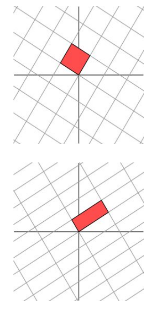
特征向量的几何含义为:对于任何的一个矩阵,我们要找到一组两两正交单位向量序列,使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。特征值的几何含义为:拉伸
其中$W$是这$n$个特征向量张成的$n$维矩阵,一般而言我们会把$W$的这$n$个特征向量标准化,即:
此时$W$就变为了标准正交基,满足:
这样我们的特征分解表达式可以写成:
2.2 奇异值的含义
特征值需要方阵,对于一个非方阵而言我们可以通过$M=AA^T$将它变为方阵,对变换后的方阵$M$求特征值的结果就是奇异值。
若$AA^T$的特征值为:
则称$\sigma {i}=\sqrt {\lambda {i}} \quad (i=1, 2, …, r)$为矩阵$A$的奇异值(注意这里只有r个)。
存在$m$阶酉矩阵$U$和$n$阶酉矩阵$V$,使得:
上式中 D的对角元叫做 A 的奇异值,U 中的列向量称为 A 的左奇异向量,V 中的列向量称为 A 的右奇异向量。
2. 奇异值分解解线性方程
2.1 解非齐次线性方程组($Ax=b$)
若矩阵的行数大于列数,则为超定方程,需要求最小二乘解,即使得$||Ax-b||_{2}$最小时的$x$,由2-范数具有酉不变性,有:
如果范数满足$║A║=║UAV║$对任何矩阵$A$以及酉矩阵$(U,V)$成立,则此范数为酉不变范数。2-范数是酉不变范数。
要让上述二范数最小,让里面的内容等于0即可。所以$Ax=b$的最小二乘解为$\left[ \begin{matrix} \Sigma & 0{r \times (n-r)} \ 0{(m-r) \times r} & 0_{(m-r) \times (n-r)} \ \end{matrix} \right] V^{T}x = U^{T}b$的最小二乘解。
令$y=V^{H}x,c=U^{H}b$,则原方程可亦表示为:
表达成矩阵形式如下:
所以$Dy=c$的最小二乘解为:
原方程组的最小二乘解为:
2.2 解齐次线性方程组($Ax=0$)
2.1的情况是让$||Ax-b||{2}$的值最小,但2.2由于$b=0$所以是让$||Ax||{2}$最小,由于$x=0$是方程的解,而我们一般不想要这个解,所以增加一个约束$||x||_2=1$,这样问题就变成了:
又因为:
令$y=V^{T}x$,则问题变为:
展开以后得到:
因为对角阵$D$的对角元素(奇异值)按递减顺序排列,所以最优解为$y=[0, 0, \cdots, 1]^{T}$(考虑到约束条件),又因为$x=Vy$,所以最优解是最小奇异值对应的$V$的列向量(右奇异向量),也就是$V$的最右边一列。比如下面的结果就是$[a_3,b_3,c_3]^T$